Hola.. Necesito una ayuda tengo este problema de geometría analítica: por favor ayudame
Este es mi problema:
"los extremos de un segmento son los puntos p1(7,4) y p2(-1,-4) hallar la
razón p1p:pp2 en que el punto p(1,-2) divide al segmento por favor necesito una
explicación del ejercicio para poder comprenderlo..
1 Respuesta
En geometría se usa mucho la razón simple en que un punto divide a otros dos. Y también se usa la razón doble que es el cociente de dos razones simples, pero eso no toca aquí.
P1p es la longitud dirigida del segmento entre el punto p1 y p
Pp2 es la longitud dirigida del segmento entre el punto p y p2
Con lo de longitud dirigida quiero decir que tiene signo. Dada una recta se asigna un sentido positivo, normalmente de izquierda a derecha y el contrario es negativo.
Asi por ejemplo pp1 = - p1p
Pue sno tenemos mas que calcular las distancias entre los puntos y darles el signo que proceda.
Lo mas sencillo será verlo con un dibujo.
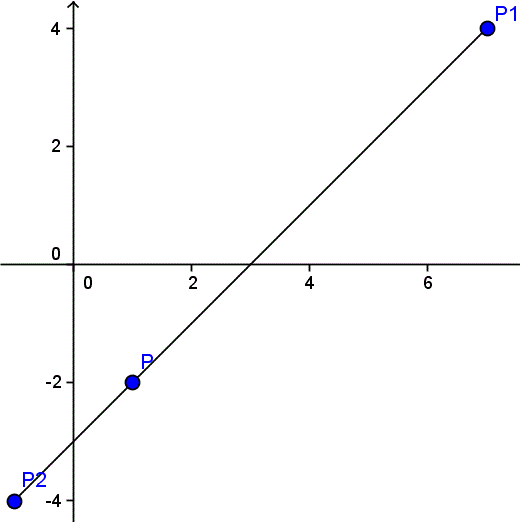
Se ve que p1p y pp2 tienen el mismo sentido haremos que los dos sean sean distancias positivas.
Y para calcular las distancias usamos la fórmula de la raíz cuadrada de los cuadrados de las diferencias de coordenadas
p1p = d[(7,4)(1,-2)] = sqrt[(7-1)^2 + (4-(-2))^2] = sqrt(6^2 + 6^2) = 6sqrt(2)
pp2 = d[(1,-2)(-1,-4)] = sqrt[(1-(-1))^2 + (-2-(-4))^2] =sqrt(2^2 +2^2) = 2sqrt(2)
Sqrt significa raíz cuadrada.
Y ya calculamos el cociente
p1p : pp2 = 6sqrt(2) / [2sqrt(2)] = 6/2 = 3
