Ejercicio de Regresión y correlación lineal

De repente me he visto con nueve problemas de correlación lineal en pocos segundos. No es posible hacerlos todos a mano y dar explicaciones en cada uno, luego lo que he hecho es crear una hoja de Excel bastante fiel a los cálculos tal como los harías a mano. Te voy a mandar una captura de pantalla del ejercicio y luego me preguntas lo que no hayas entendido y te facilito las fórmulas que no conozcas, es de suponer que las tienes en la teoría y con los datos que te aparecerán en la hoja puedas calcular los otros. Tu pregúntame todo lo que no hayas entendido y así solo explico eso porque explicarlo todo no sería más que escribir la teoría y es un poco pesado.

a)

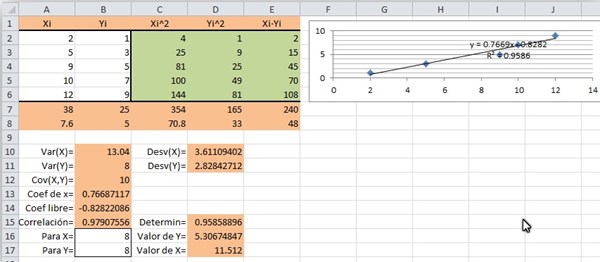
Es lo de la parte derecha

b)

Al pasar el ratón sobre la imagen te saldrá una lupa y si la pinchas la verás más grande.

A grandes rasgos, se hace una tabla con los elementos Xi, Yi, los cuadrados de ambas y el producto de las dos. Luego hay una fila con los sumatorios y otra con las medias de esos sumatorios.

La varianza se calcula asi

$$\begin{align}&V(X)=\frac{\sum_{i=1}^nX_i^2}{n}-\overline X^2\end{align}$$

Esto es la media que aparece en C8 menos el cuadrado de A8

La V(Y) se calcula de forma similar D8 - (A8)^2

La covarianza se calcula así

$$\begin{align}&Cov(X,Y)=\frac{\sum_{i=1}^nX_i·Yi}{n}-\overline X·\overline Y\end{align}$$

Y eso es  E8 - A8 · B8

La ecuación de la recta de regresión es

$$\begin{align}&y=\overline Y+\frac{Cov(X,Y)}{V(X)}(x-\overline X)\end{align}$$

En este caso

y = B8 + (B12/B10)(x-A8)

y = 5 + (10/13.04)(x-7.6)

Y operando

y = 5 + 0.76687117(x- 7.6)

y = 5 + 0.76687117x - 5.82822086

y = 0.76687117x - 0.82822086

Esa es la respuesta del apartado b. Como ves en la hoja he hecho el cálculo del coeficiente de la x y el coeficiente libre.

c)

Se aplica esta fórmula para el coeficiente de correlación. REcordar que las desviaciones son las raíces cuadradas de las varianzas

$$\begin{align}&\rho=\frac{Cov(X,Y)}{\sigma_X·\sigma_Y}=\frac {10}{3.61109402 ·2.82842712}=\\ &\\ &0.97907556\end{align}$$

Y el de determinacción es simplemente el cuadrado de este

0.97907556^2 = 0.95858896

d)

Una vez calculada la recta es muy sencillo

y = 0.76687117·8 - 0.82822086 = 6.13496936 - 0.82822086 = 5.3067485

e)

para calcular la x se hace

8 = 0.76687117x - 0.82822086

0.76687117x = 8 + 0.82822086 = 8.82822086

x= 8.82822086/0.76687117 = 11.51199994

Y eso es todo, no quería haberme extendido tanto pero creo que así lo entenderás mejor. En los próximos ejercicios ya no doy explicaciones a no ser que las pidas.