Área trapecio isósceles ABCD en función de la altura y circunradio

Al ser 120º el angulo COB la longitud del lado BC es siempre la misma, aunque en cada trapecio tenga distinta inclinación ese lado y con ello distinta altura. Inicialmente supongamos que el trapecio es un rectágulo, entonces el lado BC es vertical y el punto B se corresponde con 60º y el C con -60º.

La inclinacióndel lado BC la mediremos por el ángulo alfa que forma la perpendicular a él que pasa por el origen y el eje OX+. Entonces el punto B formará ángulo 60º+alfa y el C -60º+alfa

Hagamos el dibujo imprescindible

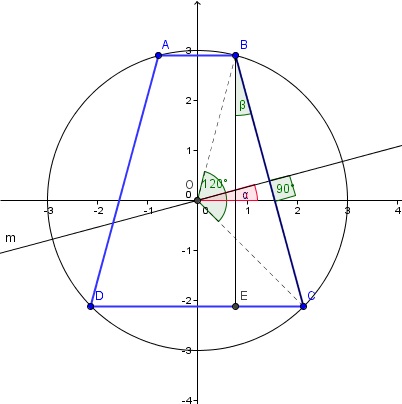
La altura del trapecio sera

h=r·sen(60º+alfa) +r|sen(-60º+alfa)| =

como alfa puede valer entre 0 y 30º

= r·sen(60º+alfa) + r·sen(60º-alfa) =

r[sen(60º+alfa) +sen(60º-alfa)] =

r[sen60º·cos(alfa)+cos60º·sen(alfa) + sen60º·cos(alfa)-cos60º·sen(alfa)] =

2r(sen60º·cos(alfa)) =

sqrt(3)·r·cos(alfa)

Resumiendo

$$\begin{align}&h=\sqrt 3\;r·\cos\alpha\end{align}$$

Ahora calculemos la base inferior y superior

La inferior es

B = 2r·cos(-60º+alfa) = 2r·cos(alfa-60º)

y la superior es

b = 2r·cos(60º+alfa)

Por lo que el área del trapecio será

$$\begin{align}&A=\frac{(B+b)h}{2}=\\ &    \\ &    \frac{2r·[\cos(\alpha-60º)+\cos(\alpha+60º)]\sqrt 3\;r·\cos\alpha}{2}=\\ &    \\ &    \sqrt 3r^2cos\alpha(\cos\alpha·cos60º+sen\alpha·sen60º+\cos\alpha·cos60º-sen\alpha·sen60º)=\\ &    \\ &   \sqrt 3 \;r^2 \cos \alpha·2cos\alpha ·cos60º=\\ &    \\ &    \sqrt 3\;r^2cos^2\alpha\\ &    \\ &    \text{Resumiendo}\\ &    \\ &    A=\sqrt 3r^2cos^2\alpha\\ &   \\ &   \text {como teníamos}\\ &   \\ &   h=\sqrt 3\;r·\cos\alpha\\ &   \\ &   \cos\alpha =\frac{h}{\sqrt 3\;r}\\ &   \\ &   \text{por lo que}\\ &   \\ &   A=\sqrt 3\; r^2\left(\frac{h}{\sqrt 3\;r}  \right)^2 =\frac{h^2}{\sqrt 3}\\ & \\ & \text{o para los puristas}\\ & \\ & A=\frac{h^2 \sqrt 3}{3}\end{align}$$

No es necesario el circunradio ya va implícito en la altura.
-----------------------------------------

Vamos a comprobar que esto es verdad al menos para los dos trapecios extremos.

Con alfa=0 tenemos el rectangulo de altura

h=2rsen60º = r·sqrt(3)

y base

B=b=2rcos60º

El areá es

A = 4r^2sen60º·cos60º = 4r^2sqrt(3)/4 = r^2·sqrt(3)

y

h^2/sqrt(3) = r^2·3/sqrt(3) = r^2·sqrt(3)

se cumple

Y el otro extremo es cuando alfa=30º y se foma un triaángulo equilatero de 

h=r +(1/2)r) = 3r/2

y base = 2·cos30º= sqrt(3)·r

el area es

A= [(3r/2)sqrt(3)·r]/2 = r^2·[3sqrt(3)/4]

y

h^2/sqrt(3) = (9r^2/4)/sqrt(3) = r^2[3sqrt(3)/4]

Luego se cumple.

------------------------------------

Así que sin lugar a dudas la fórmula es

$$\begin{align}&A =\frac{h^2}{\sqrt 3}=\frac{h^2 \sqrt 3}{3}\end{align}$$

·

Y eso es todo.