Ejercicio sistema de inecuaciones no entiendo :z

Debemos dibujar las dos rectas que liimitan las czonas de cumplimiento de las desigualdades

Para la recta

2x-y=4

tomando x=0 quea -y=4 ==> y=-4

luego el punto (0,4) es de la recta

Y haciendo y =0 queda  2x=4  ==> x=2

Luego el punto (2,0) pertenece a la recta.

Y con esos dos puntos se puede pintar

Y para la  recta y=3(x-1)

si hacemos x=0 queda y=-3 luego (0,-3) pertenece a la recta

y si hacemos y=0 queda 3(x-1)=0  ==> x-1= 0   ==> x =1

luego el punto (1,0) pertenece a esa recta

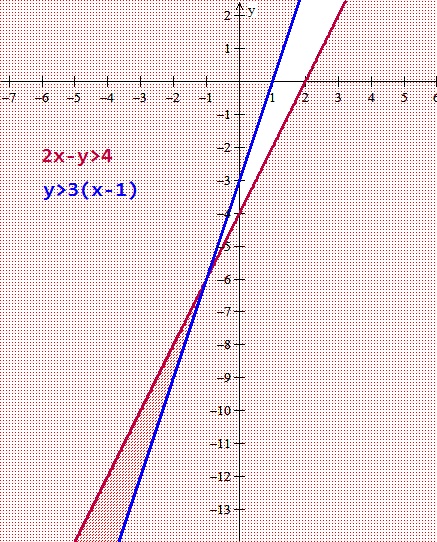
Y ahora tomamos un punto externo a las rectas para comprobar si su zona es la que cumple la desigualdad o no

Yio tomo (0,0) siempre que se pueda

Para la primera recta, la roja

2·0 - 0 = 0 > 4 es falso luego la zona que se sombrea es la que no tiene (0,0) que es la derecha de la recta roja

Y para la recta azul

0>3(0-1)

0>-3

Es verdadero luego la zona del (0,0) es la buena y sombreamos la izquierda de la zona azul.

Y la zona doblemente sombreada es la solución que es el triangulo que se be abajo y toda su prolongación en el plano.

Como las desiugualdades son estrictas la frontera de las rectas no entra en la soilución.

·

Y eso es todo.