$$\begin{align}& \end{align}$$¡Hola Oscarito!
·
La principal medida de dispersión es la desviación estándar, por el camino también se calculará la varianza. Y otra medidas de dispersion son el rango y el recorrido intercuartítico.
Vamos con lo duro.
La varianza aparece definida siempre así:
$$\begin{align}&\sigma^2=\frac{\sum_{i=1}^n(X_i-\overline x)^2·n_i}{\sum_{i=1}^n n_i}\\&\\&\end{align}$$Bueno, en realidad la fórmula que se usa es para datos sueltos y entonces n es el número de datos y queda más simplificada.
$$\begin{align}&\sigma^2=\frac{\sum_{i=1}^n(X_i-\overline x)^2}{n}\end{align}$$Pero si tuvieramos que hacerlo a mano usaríamos la primera ya que se repiten muchos datos.
Pero lo que quería decir es que aunque sea esa la definción en la practica se usa una fórmula que es igual pero las cuentas son más sencillas de hacer para las personas
$$\begin{align}&\sigma^2=\frac{\sum_{i=1}^nn_i·X_i^2}{\sum_{i=1}^n n_i}-\overline x^2\\&\\&\text {o más fácil de acordarse la de datos sueltos}\\&\\&\sigma^2=\frac{\sum_{i=1}^n X_i^2}{n}-\overline x^2\end{align}$$Y para resolverlo a la tabla anterior añadimos una columna que calcula los valores
ni·(Xi)^2 en cada fila y luego los suma
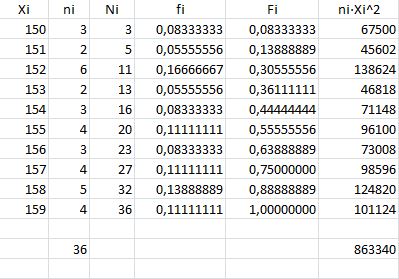
La varianza será
$$\begin{align}&\sigma^2= \frac{863340}{36} - (154.833333)^2 =\\&\\&23981.66666 - 23973.36111 =8.30555\\&\\&\text{Y la desviación estandar es:}\\&\\&\sigma= \sqrt{8.30555}= 2.8819\end{align}$$El rango o recorrido es 159-150 = 9
Y el recorrido intercuartílico es el tercer cuartil menos el primero
El primero es el valor que ocupa el 10 lugar, mirando en la tabla es 152 y el tercero corresponde al dato con ordinal 28 que es 158
Luego el recorrido intercuartílico es 158-152 = 6
·
Y eso es todo.

