Como se resuelven las Integrales definidas y por sustitución?
Me pueden ayudar con esto por favor, les agradezco mucho.
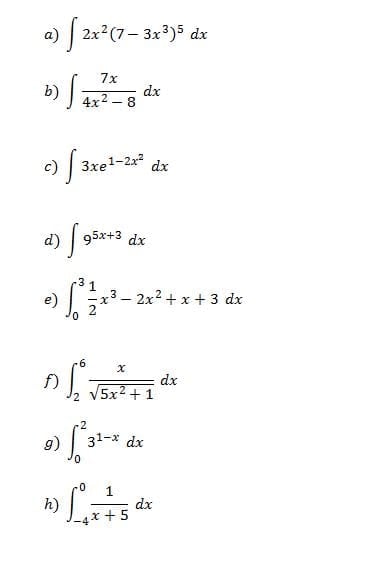
3 respuestas
Respuesta de Lucas m
3
$$\begin{align}&a)\\&\int 2x^2(7-3x^3)^5dx= \int \frac{-3}{-3}2x^2(7-3x^3)^5dx=\\&\\&\frac{-1}{3}\int -6x^2(7-3x^2)^5dx=\\&\\&\frac{-1}{3}·\frac{(7-3x^3)^6}{6}+C= -\frac{(7-3x^3)^6}{18}+C\\&\\&b) 7 \int \frac{8}{8} · \frac{x}{4x^2-8}dx=\frac{7}{8} \int \frac{8x}{4x^2-8}=\\&\frac{7}{8}ln|4x^2-8|+C\\&\\&c) 3 \int \frac{-4}{-4}xe^{1-2x^2}dx=-\frac{3}{4} \int -4xe^{1-2x^2}dx=\\&\\&\frac{-3}{4}e^{1-2x^2}+C\\&\\&d) \int 9^{5x+3}dx= \frac{9^{5x+3}}{5·ln9}+C\\&\\&\end{align}$$Hola Miryam!
Te hago las 4 primeras. Mándame el resto en dos preguntas más.
Me es más cómodo con el editor de ecuaciones.
No me he dado cuenta, y no están hechas por sustitución, sino directamente.
Si no te sirve, vuelve a mandarlas y te las hago en un momento.
Respuesta de Valero Angel Serrano Mercadal
3
·
Te iba a decir lo mismo, que no se pueden mnandar tantos ejercicios tantos. Yo te iba a hacer alguna menos que Lucas pero haré las mismas y el resto en dos preguntas, así se recompensa mejor el trabajo.
$$\begin{align}&a)\quad \int 2x^2(7-3x^3)^5dx=\\&\\&t=7-3x^3\\&dt=-9x^2dx \implies x^2dx =-\frac 19dt\\&\\&2\left(-\frac 19\right)\int t^5 dt =\\&\\&-\frac 29·\frac{t^6}{6}+C = -\frac{(7-3x^3)^6}{27}+C\\&\\&\\&\\&\\&b)\quad \int \frac{7x}{4x^2-8}dx=\\&\\&t=4x^2-8\\&dt=8xdx\implies xdx=\frac 18dt\\&\\&=7·\frac 18 \int \frac {dt}{t}=\frac 78lnt+C=\\&\\&\frac 78ln(4x^2-8)+C\\&\\&\\&\\&\\&c)\quad \int 3xe^{1-2x^2}dx=\\&\\&t=1-2x^2\\&dt = -4xdx \implies xdx=-\frac 14 dt\\&\\&=3·\left(-\frac 14 \right)\int e^t dt\\&\\&=-\frac 34e^t+C=-\frac 34e^{1-2x^2}+C\\&\\&\\&\\&\\&d)\quad \int 9^{5x+3}dx=\\&\\&t=5x+3\\&dt=5dx\implies dx = \frac{1}{5}dt\\&\\&=\frac 15\int 9^tdt=\frac 15·\frac{1}{ln9}\int 9^t·ln9\;dt=\\&\\&\frac{9^t}{5·ln9}+C = \frac{9^{5x+3}}{5·ln9}+C\\&\\&\end{align}$$Y eso es todo.
