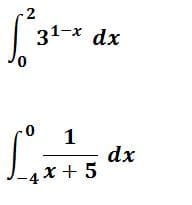Como puedo resolver las siguientes 2 integrales?

·

Es que a los profesores a veces no les gusta si las haces de forma distinta a como te han enseñado.

Entonces yo aquí podría resolverlas de 4 formas.

Primero, no cosnsidero que las integrales tengan suficiente entidad para resolverlas por cambio de variable, luego con un poquitín de sentido común salen.

Sabemos que

$$\begin{align}&(3^{1-x})' = 3^{1-x}·ln3·(-1)= -ln3·3^{1-x}\\&\\&\text{y para que eso sea el integrando debemos} \\&\text{multiplicar por una constante y así la}\\&\text{derivada sería}\\&k(-ln3)·3^{1-x}=3^{1-x}\\&k·(-ln3) = 1\\&k = -\frac 1{ln3}\\&\\&\text{con lo cual la integral es}\\&\\&\left.-\frac{1}{ln3}·3^{1-x}\right|_0^2=\\&\\&-\frac{1}{ln3}·(3^{1-2}-3^{1-0})=\\&\\&-\frac{1}{ln3}(3^{-1}-3^1)=\\&\\&-\frac{1}{ln3}\left(\frac 13-3  \right)=\\&\\&-\frac{1}{ln3} ·\frac{-8}{3}= \frac{8}{3\,ln3}\\&\\&\text{Si quieres hasta puedes poner }\\&\\&\frac 8{ln\, 27}\end{align}$$

Y con la segunda no vas a tener tanto lío, todo el mundo está de acuerdo nada más que la ve que la integral es

ln|x+5|

Bueno, algunos no ponen el valor absoluto, pero lo hacen mal.

Y entonces la integral definida es

ln|0+5| - ln|-4+5| = ln5 - ln1 = ln5