Halle la elevación del globo en ese instante y la distancia del globo a cada observador
Dos personas se encuentran alejadas entre sí 5 km en una llanura, y un cierto instante, un globo aerostático atraviesa entre ambos. Cada individuo mide el ángulo de elevación con el que ve el globo y resulta 52 grados 35 min y 67 grados y 42 min respectivamente. Halle la elevación del globo en ese instante y la distancia del globo a cada observador.
Este ejercicio es de la junta de castilla y león en las pruebas de acceso a ciclos formativos de grado superior en el año 2010.
2 Respuestas
Respuesta de Valero Angel Serrano Mercadal
1
Respuesta


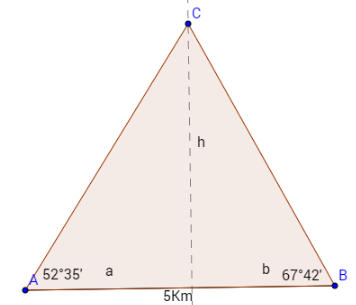
Profe, d1 es imposible ya que d1+d2 = 5 (pero d1>5). - Anónimo
Las distancias al globo son AC y BC de tu dibujo, suman más de 5 - Valero Angel Serrano Mercadal
puf...lo otro que calculé yo fueron las distancias a, b, las proyecciones del globo sobre la horizontal...eso por no leer lo que preguntan :) - Anónimo
No sé lo que hiciste, pero fíjate que la altura ya la calculaste mal. Saludos - Valero Angel Serrano Mercadal