Resolver el triangulo con la ley de senos
Me podrías ayudar por favor con el punto 9.
Resolver el triangulo usando la ley de senos

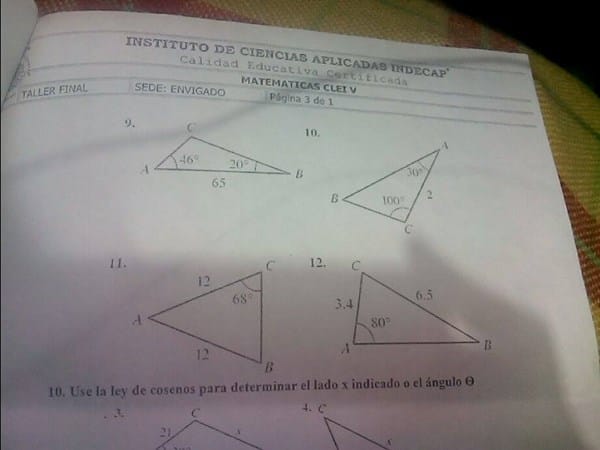
2 Respuestas
Respuesta de Lucas m
2
Respuesta de Valero Angel Serrano Mercadal
1
