Encontrar la distribucion de Poisson del siguente ejercicio
¿Podrian explicarme como aplico Poisson con estos datos?
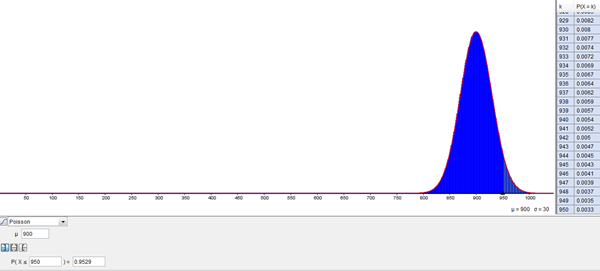
Sea X una variable aleatoria que sigue una distribución de poisson de parámetro ʎ= 900 Calcular (PX<950)
3 Respuestas
Supongo que lo sabes, pero por las dudas lo planteo
$$\begin{align}&Puntual\\&p(x) = {e^{-\lambda}\lambda^x \over x!}\\&Acumulado\\&p(x \le X) = \sum_{k=0}^{X}{e^{-\lambda}\lambda^k \over k!}\\&\\&En\ este\ caso\\&p(x \le 950) = \sum_{k=0}^{950}{e^{-900} 900^k \over k!}\\&\\&\end{align}$$Como verás ese cálculo no es simple, yo voy a usar Excel para calcular este valor
=POISSON.DIST(900;950;VERDADERO)
Que da como resultado: 0,0532
Con GeoGebra el resultado es
0.9529
$$\begin{align}& \end{align}$$¡Hola Giovanni!
·
Muchos de estos problemas proceden de la antiguedad. Hace 30 años no había un mal PC, si acaso en las universidades había un triste ordenador central dando servicio a centenares de usuarios.
En aquel entonces lo que se usaba hasta la saciedad a todas las horas era una hojita que contenía la distribución normal N(0,1) y no había otra cosa para resolver estos problemas. Entonces se inventaban aproximaciones más o menos buenas a la distribución normal, ahora las vemos como malas pero entonces eran grandes logros.
Entonces para la distribución de Poisson también había su aproximación a una distribución normal, en concreto a una normal de media lambda y desviación raíz de lambda.
$$\begin{align}&P(\lambda) \sim N(\lambda,\sqrt \lambda)\\&\\&P(900)\sim N(900,30)=X\\&\\&P(X\lt 950)=P\left(Z\lt \frac{950-900}{30}\right)=\\&\\&P(Z\lt 1.6666...)=0,952208985\end{align}$$Que como puedes ver tiene los tres primeros decimales exactos, una aproximación muy buena las he visto mucho peores.
Luego eso, que este ejercicio soo tiene sentido en la antiguedad y la solución que quisieron que le dieras es estas que te he dado yo.
Por cierto, con Excel la fórmula es:
=POISSON.DIST(950;900;1)
Y el resultado
0.95288098