Máximos, mínimos y gráfica de una función URGE

·

Como siempre en estos casos, derivaremos la función, la igualaremos a 0 y calcularemos las raíces si se puede.

f '(x) = 5x^4 - 5 = 0

5x^4 = 5

x^4 = 1

Esto son las raíces cuartas de la unidad, hay cuatro, dos son reales {-1,1} y las otras dos son imaginarias {-i, i}

Si no conocces esto de los números complejos puedes hallar las raíces factorizado

x^4 = 1

x^4 - 1 = 0

(x^2+1) (x^2 -1) = 0

(x^2+1)(x+1)(x-1)=0

x^2+1 no tiene raíces reales es siempre positivo.

Por lo tanto las raíces son -1 y 1

Ahora calculamos la derivada segunda para ver si son máximos o mínimos

f''(x) = 20x^3

entonces

f''(-1) = 20·(-1)^3 = 20·(-1) = -20 < 0  Luego es un máximo

f''(1) = 20·1^3 = 20 >0  Luego es un mínimo

Y los valores de la función son

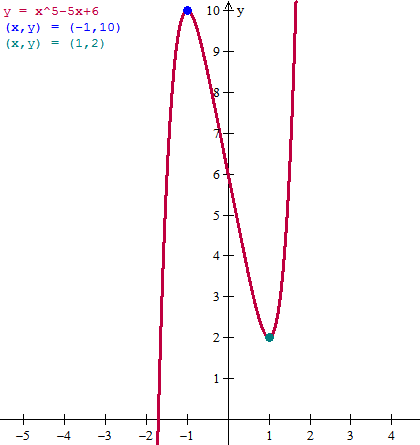
f(-1) = (-1)^5 - 5·(-1) + 6 = -1+5+6 = 10

f(1) = 1^5 -5·1 +6 = 1-5+6 = 2

Por tanto hay un máximo relativo en (-1, 10)

Y hay un mínimo relativo en (1, 2)

Y eso es todo.