Gráfica de una función, graficar la curva URGE

·

Es un polinomio luego el dominio es todo R y es continua en todo R.

·

Es un polinomio de grado impar, por lo tanto en -infinito vale -infinito y en +infinito vale +infinito.

·

Además es una función impar porque

f(-x) = -f(x)

f(-x) = (-x)^3 - 4(-x) = - x^3 + 4x = -(x^3-4x) = -f(x)

Luego tiene simetria central, respecto al punto (0,0)

·

Los cortes con el eje X son

x^3-4x=0

x(x^2 - 4)=0

x(x+2)(x-2)=0

Los cortes son (0,0), (-2,0), (2,0)

El corte con el eje Y ya está incluido, es (0,0)

·

Los máximos y mínimos son

$$\begin{align}&f'(x) = 3x^2 - 4 =0\\&\\&3x^2 = 4\\&\\&x^2=\frac 43\\&\\&x=\pm \sqrt{\frac 43}= \pm \frac{2}{\sqrt 3}= \pm \frac{2 \sqrt 3}{3}\\&\\&f''(x) = 6x\\&\\&f''\left(\frac{2 \sqrt 3}{3}  \right)=\frac{12 \sqrt 3}{3}=4 \sqrt 3\gt0\implies mínimo\\&\\&f''\left(-\frac{2 \sqrt 3}{3}  \right)=-\frac{12 \sqrt 3}{3}=-4 \sqrt 3\gt0\implies máximo\\&\\&f\left(\frac{2 \sqrt 3}{3}  \right)=\left(\frac{2 \sqrt 3}{3}  \right)^3-4\left(\frac{2 \sqrt 3}{3}  \right)=\frac 89 \sqrt 3-\frac 83 \sqrt 3=\\&\\&-\frac {16}{9} \sqrt 3\approx -3.0792\\&\\&f'\left(-\frac{2 \sqrt 3}{3}  \right)= \frac {16}{9} \sqrt 3\approx 3.0792\text{ por simetría central}\\&\\&\text{máximo relativo }  \left(-\frac{2 \sqrt 3}{3},\frac {16}{9} \sqrt 3  \right)\approx (-1.1547,\;3.0792)\\&\\&\text{mínimo realtivo }\left(\frac{2 \sqrt 3}{3},-\frac {16}{9} \sqrt 3  \right)\approx (1.1547,\;-3.0792)\\&\\&\text{Para intervalos de crecimiento o decrecimiento}\\&\\&\left(-\infty,-\frac{2 \sqrt 3}{3}  \right) \text{creciente porque termina en máximo}\\&\\&\left(-\frac{2 \sqrt 3}{3},\frac{2 \sqrt 3}{3}  \right) \text{decreciente porque termina en mínimo}\\&\\&\left(\frac{2 \sqrt 3}{3},\infty  \right)  \text{Creciente porque empieza en un mínimo}\\&\\&\\&\text{Para calcular puntos de inflexión, la derivada segunda es}\\&\\&f''(x)=6x =0\\&\\&x=0 \text{ es punto de inflexión es el (0,0)}\\&\\&\text{Para el tipo de concavidad}\\&\\&\text{Para x}\lt0\implies f''(x)\lt 0\implies \text{cóncava hacia abajo}\\&\\&\text{Para x}\gt0\implies f''(x)\gt 0\implies \text{cóncava hacia arriba}\end{align}$$

Y la gráfica es:

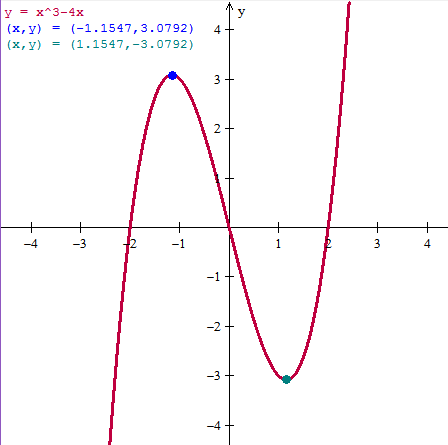
Y eso es todo.