Siguiente ejercicio de representar función

Sigue con la puntuación baja mi respuesta en esta pregunta.

Cómo representar las siguientes funciones?

Súbela por favor.

·

El dominio es todo R, los polinomios no tienen problemas en ningún punto, el valor absoluto tampoco.

Veamos antes de nada si corta al eje X

f(x) = |x^2 - 4x + 3|

Es de fácil factorización

f(x) = |(x-1)(x-3)|

corta a los ejes en los puntos x=1 y x=3

Y por lo tanto vale 0 en algún punto y tiende a +infinito en -infinito e infinito. Como es continua tiene que tomar todos los valores intermedios entre 0 y +infinito, y ninguno más porque nunca es negativa, por lo tanto la imagen es

Im f = [0, +infinito)

La figura sin valores absolutos es una parábola en forma de U cuyo vértice sería 

f'(x) = 2x-4=0  ==> x = 2

Al tomar el valor absoluto la parte de debajo del eje X se refleja sobre él, cono lo que los intervalos de crecimiento y decreciniento quedan así

(-infinito, 1)    decreciente

(1, 2) creciente

(2,3) decreciente

(3, +infinito) creciente.

Los extremos absolutos son:

Máximo absoluto no existe, tiende a infinito

Mínimo absoluto 0 en los puntos x=1 y x=2

Máximo relativo en x=2 cuyo valor es

f(2) = |2^2-4·2+3| = |4-8+3| = 1

Mínimos relativos, los mismos que los absolutos.

Asíntotas de ningún tipo, los polinomios de grado >=2 no tienen ninguna asíntota y al tomar el valor absoluto tampoco.

·

Los cortes con los ejes ya se calcularon con el eje V que son (1,0) y (3,0)

Y el corte con el eje Y es

|0^2 - 4·0 + 3| = 3

Y con esto y algún punto más si quieres calcular la gráfica es esta

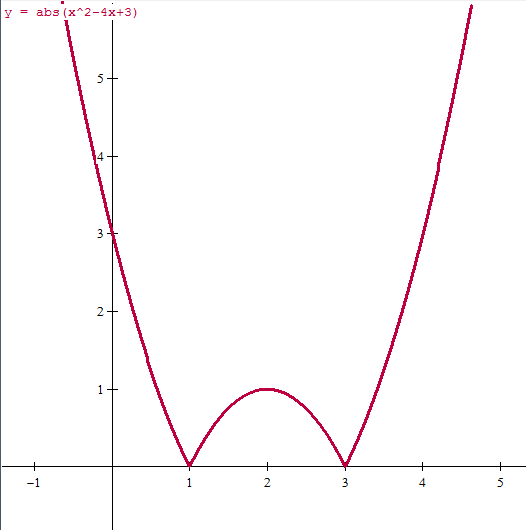
Y eso es todo, espero que te sirva y lo hayas entendido.

No olvides subir la puntuación de

http://www.todoexpertos.com/preguntas/64qdie84l8dauonk/como-representar-las-siguientes-funciones?selectedanswerid=64qwmjnda7tw5cd5

Para poder contestarte más preguntas.