Cómo representar la siguiente función

Mery, antes que nada te comento que las respuestas que están bien contestadas de manera correcta debes calificarlas como Excelente (si tienes intenciones que los expertos sigan colaborando contigo). Más allá de este comentario, vamos al ejercicio...

Como te piden hacer la gráfica también, voy a empezar con esto, que de ahí creo que será más fácil deducir algo de lo que están pidiendo...

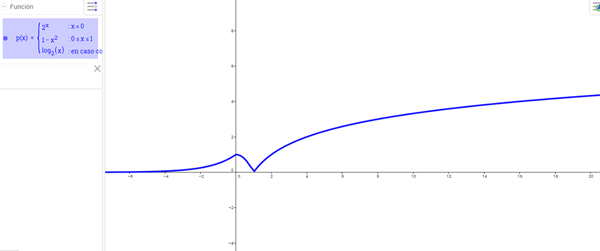
La función es partida pero inicialmente está definida para todos los valores, además tenemos que 2^x y 1-x^2 están definidas para todos los valores, y el Log(x) es definida solo para los valores positivos, pero en este caso no tenemos inconvenientes pues la definen para los valores a partir del 1.

Si bien no lo piden, se puede ver también que la función es continua y esto se puede ver porque:

$$\begin{align}&x=0 \to\\&2^0=1 \land 1-0^2 = 1 \to continua\\&\\&x=1\\&1-1^2=0 \land log_2\ x = 0 \to continua\\&\\&\mbox{analicemos la función de a trozos}\\&x<0\\&f(x)=2^x:\mbox{es estrictamente creciente}\\&lim_{x \to -\infty} 2^x \to 0\\&lim_{x \to 0^-} 2^x \to 1\\&\mbox{El rango hasta 0 es el intervalo (0,1)}\\&\\&0\le x<1\\&f(x)=1-x^2\\&f'(x)=-2x \mbox{ Vale cero en x=0 y para el resto de los valores es negativa, así que la función es decreciente en ese intervalo}\\&f(0)=1\\&f(1)=0\\&\mbox{El rango entre 0 y 1 es el intervalo (0,1)}\\&\\&x \ge1\\&f(x)=log_2(x)\\&\mbox{La función es estrictamente creciente y además}\\&f(1) =log_2(1)=0 \\&lim_{x \to +\infty} log_2(x) \to +\infty\\&\mbox{El rango para f(x) mayor que 1 es el intervalo (0,} +\infty)\\&\mbox{De todo lo anterior creo que podemos deducir:}\\&Dominio: \mathbb{R}\\&Rango: (0,+\infty)\\&Monotonía:\\&Crece: (-\infty,0) \mathbb{U} (1,+\infty)\\&Decrece: (0,1)\\&Asíntotas:\\&Horizontales: 0 \mbox{ (cuando x tiende a }-\infty\\&Verticales\ y \ Oblicuas: \ no \ tiene\\&Extremos: \mbox{máximo local en x=0 f(0)=1 y mínimo local en x=1 f(1)=0}\\&\mbox{Corte con los ejes:}\\&y=0 \mbox{ La función no corta el eje x}\\&x=0 \mbox{ La función corta al eje y en f(0)=1}\\&\\&\\&\\&\end{align}$$