Calculo integral resolver la siguiente integral indefinida paso a paso
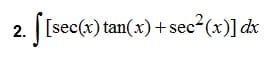
Resolver la siguiente integral indefinida paso a paso teniendo en cuenta las propiedades de las integrales
2 respuestas
Respuesta de Lucas m
1
Respuesta de Valero Angel Serrano Mercadal
1
