Soluciones a este problema de Geometria analitica amigos?
Los vértices de un triángulo son A(-4,1); B(-3,3) y C(3,-3). Hallar la longitud de la altura del vértice A sobre el lado BC y el área del triángulo ; 9
1 Respuesta
Respuesta de Lucas m
1
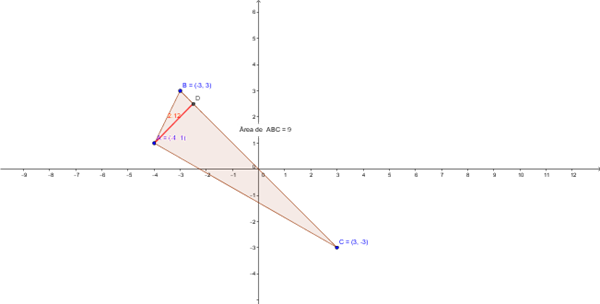
Ecuación Continua de la recta BC:
$$\begin{align}&\frac{x-x_o}{v_1}=\frac{y-y_o}{v_2}\\&\\&\vec{BC}=C-B=(3,-3)-(-3,3)=(6,-6)\\&\\&\frac{x-(-3)}{6}=\frac{y-3}{-6}\\&\\&\frac{x+3}{6}=\frac{y-3}{-6}\\&\\&-6(x+3)=6(y-3)\\&Simplificando:\\&-(x+3)=y-3\\&-x-3=y-3\\&y=-x \ \ (bisectriz \ del \ 2º \ y \ 4º \ cuadrante)\\&Ecuación \ General:\\&x+y=0 \ \ \ (r)\\&\\&h_A=dist(A,r)=\frac{|Ax_o+By_o+C|}{\sqrt{A^2+B^2}}=\frac{|1(-4)+1(1)|}{\sqrt{1^2+1^2}}=\frac{3}{\sqrt 2}\\&\\&Area=\frac{1}{2}base·h=| \vec{BC}|·h_A=\frac{1}{2}\sqrt{6^2+(-6)^2}·\frac{3}{\sqrt 2}=\frac{1}{2} \sqrt{72}· \frac{3}{\sqrt 2}=\\&\\&\frac{3}{2}·\frac{\sqrt{72}}{\sqrt 2}=\frac{3}{2}\sqrt{\frac{72}{2}}=\frac{3}{2}\sqrt{36}=\frac{3}{2}(6)=9\ \ u^2\\&\\&\\&\\&\end{align}$$Saludos:
:
:
