Vectores A de 25Ib de modulo y que forma un angulo de 30 B de 42Ib de modulo y que forma un angulo de 50
Construir un esquema y estimar visualmente elmodulo y el angulo del vector C de forma que 2A+C-B sea un vector de 35Ib de modulo orientado según la dirección positiva del eje x
1 Respuesta
Respuesta
1
Creo que tu profesor se está burlando de tí para hacerte hacer esto :), pero bueno. Te dejo los vectores originales
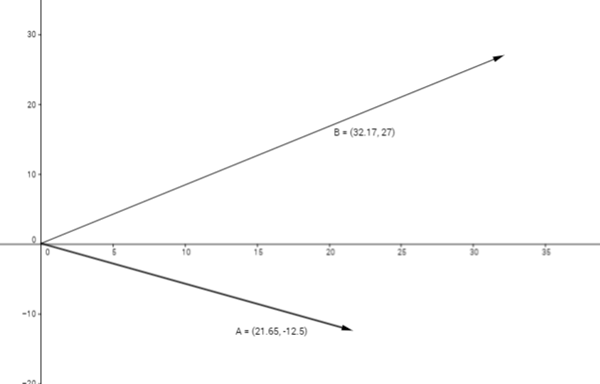
La estimación te la dejo, yo voy a resolver el punto b) que es resolverlo de manera exacta.
$$\begin{align}&R = 2A + C - B\\&(35, 0) = 2(25cos(-30°), 25sen(-30°)) + (C_x, C_y) - (42cos(40°), 42sen(40°))\\&\text{Si tienes duda con el planteo anterior avisa, pero lo que hice fuí escribir los datos que nos dieron como}\\&\text{coordenadas, considerá que 50° en sentido horario desde el eje +Y es l mismo que 40°}\\&\text{Sigo con las cuentas}\\&(35, 0) = (50cos(-30°), 50sen(-30°)) + (C_x, C_y) - (42cos(40°), 42sen(40°))\\&\text{Igualo cada una de las coordenadas}\\&35 = 50cos(-30) + C_x - 42cos(40)\\&0 = 50sen(-30) + C_y - 42sen(40)\\&\text{Y ahora son todos números, voy a usar 4 decimales}\\&C_x = 35 - 43.3013+32.1739 = 23.8726\\&C_y = 25+26.9971 = 51.9971\\&\text{y el vector C es (23.8726,51.9971) que si lo querés expresar como módulo y ángulo, sería}\\&|C| = \sqrt{23.8726^2+51.9971^2}= 57.2154\\&\alpha = ArcTan(\frac{51.9971}{23.8726}) = 65°339\end{align}$$