Un triángulo tiene como vértices a

·

·

¡Hola Miriam!

Esta es la gráfica. Los ángulos están calculados por el propio programa, servirán para comprobar si hacemos bien las cuentas.

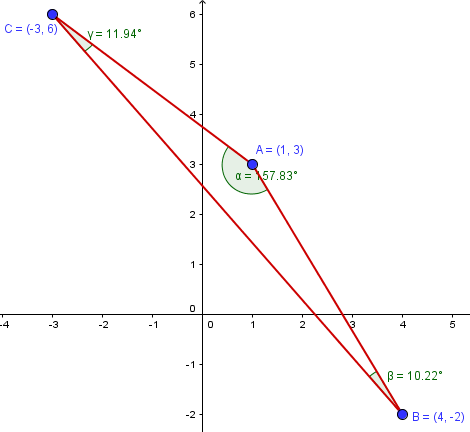
Y para calcular los angulos usaremos que:

$$\begin{align}&\vec u·\vec v= |\vec u|\;|\vec v|\;\cos(\vec u,\vec v)\\&\\&\cos(\vec u,\vec v)=\frac{\vec u·\vec v}{ |\vec u|\;|\vec v|}\\&\\&\vec{AB}=(4,-2)-(1,3) = (3,-5)\\&\vec{AC}=(-3,6)-(1,3)=(-4,3)\\&\vec{BC}=(-3,6)-(4,-2)=(-7,8)\\&\\&cosA=\frac{\vec {AB}·\vec{AC}}{|\vec{AB}|\;|\vec{AC}|}=\\&\\&\frac{(3,-5)·(-4,3)}{\sqrt{3^2+5^2}\sqrt{4^2+3^2}}=\frac{-12-15}{\sqrt{34}·5}=\\&\\&-\frac{-27}{5 \sqrt{34}}=-\frac{27 \sqrt{34}}{170}\approx -0.9260923598\\&\\&\text{Y comprobamos que}\\&\cos^{-1}(-0.9260923598)=157.8336542\\&\\&\text{luego se corresponde con la gráfica}\\&\\&\\&\\&cosB=\frac{\vec {BA}·\vec{BC}}{|\vec{BA}|\;|\vec{BC}|}=\\&\\&\text{Tener en cuenta que }\vec {BA}=-\vec {AB}\\&\\&\frac{(-3,5)·(-7,8)}{\sqrt{3^2+5^2}\sqrt{7^2+8^2}}=\frac{21+40}{\sqrt{34}·\sqrt{113}}=\\&\\&\frac{61}{\sqrt{3842}}=\frac{61 \sqrt{3842}}{3842}\approx 0.9841270174\\&\\&\text{Y comprobamos }\\&\cos^{-1}(0.9841270174)=10.22216863\\&\text{Está bien.}\\&\\&\\&\\&cosC=\frac{\vec {CA}·\vec{CB}}{|\vec{CA}|\;|\vec{CB}|}=\\&\\&\text{Tener en cuenta que }\vec {CA}=-\vec {AC},\;\vec{CB}=-\vec{BC}\\&\\&\frac{(4,-3)·(7,-8)}{\sqrt{4^2+3^2}\sqrt{7^2+8^2}}=\frac{28+24}{5·\sqrt{113}}=\\&\\&\frac{52}{5 \sqrt{113}}=\frac{52 \sqrt{113}}{565}\approx 0.9783497031\\&\\&\text{Y comprobamos }\\&\cos^{-1}(0.9783497031)=11.94417719\\&\text{Está bien}\end{align}$$

Luego todo está bien.

Saludos.

:

: