Determinar el limite de lim┬(x→2)
En la siguiente ecuación, para poder hallar el valor del limite cuando x=2
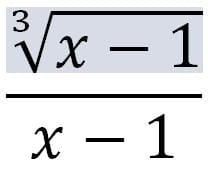
2 Respuestas
·
·
¡Hola Myriam!
Ya te asegurarás si es ese el enunciado porque calcular ese límite cuando x tiende a 2 no tiene ningún mérito. Como la función es continua en x=2 será el valor de la función en ese punto.
\
$$\begin{align}&\lim_{x\to 2} \frac{\sqrt[3]{x-1}}{x-1}=\frac{\sqrt[3]{2-1}}{2-1}=\frac{\sqrt[3]{3}}{1}=\sqrt[3]3\end{align}$$Y eso es todo, saludos.
:
:
Anda que se necesita tanto vídeo como te ha dado JH para resolver este límite. Menos le hubiera costado resolverlo que copiar y pegar la respuesta vale para todo que tiene. ¿O es que no sabe resolverlos? Y además prohibe los comentarios míos en sus respuestas, ¿de qué puede tener miedo?
He hecho una lista con las personas que votan a Herrera por sus respuestas que no son respuestas, son el "háztelo tu mismo con el primer enlace que me ha salido en el buscador".
Yo creo que es una injusticia grándisima que se vote por eso y mucho más que se vote excelente. Y como me parece mal, he decidido que los que le votáis a él no apreciáis la labor de los expertos de verdad y no merecéis contestaciones de estos. Luego yo no te contestaré ninguna pregunta más mientras vea esos puntos de aquí de Herrera que me hacen mal a los ojos y sobre todo al alma. Quítaselos si quieres que vuelva a contestarte.
Estimada amiga: En los siguientes enlaces que seleccioné para ti encontrarás la forma de resolverlo:
http://html.rincondelvago.com/limites-de-funciones.html
http://www.ehu.eus/juancarlos.gorostizaga/apoyo/limites.htm