¿Un cliente hace 10 depósitos mensuales de $200.000 al principio de cada mes, iniciando hoy?...

·

·

¡Hola Angelita!

Al final del décimo mes el valor de su capital será el de una renta prepagable de 10 meses

$$\begin{align}&V_{n}=c(1+i)\times \frac{(1+i)^n-1}{i}\\&\\&V_{10}= $200\,000(i+1)\times \frac{(1+i)^{10}-1}{i}\\&\\&\text{Y al terminar el mes 24 su valor será}\\&\\&V_{24}= V_{10}·(1+i)^{14}\\&\\&$6\,000\,000=$200\,000(1+i)^{15}\times \frac{(1+i)^{10}-1}{i}\\&\\&30=\frac{(1+i)^{25}-(1+i)^{15}}{i}\\&\\&30i-(1+i)^{25}+(1+i)^{15}=0\end{align}$$

No es tan importante como dejemos la ecuación, sabemos qie no podemos hacerla y habrá que usar el ordenador para resolverla.

Esta vez voy a usar la función Buscar Objetivo de Excel.

Aquí tienes los datos metidos en la ventana de buscar objetivo y en la barra de fórmulas está la fórmula de la celda 1. En la celda A2 no se puede meter 0 porque 0 es solución de la ecuación y se queda en ella, puedes poner 0,1 por ejemplo, yo puse 1 para estar seguro que antes que la solución i=0 encuentra la solución que de verdad buscamos

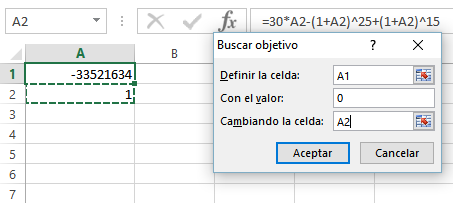
Y tras pulsar aceptar saldrá esto.

En A2 está la respuesta y A1 nos dice como de próxima se a quedado la función del objetivo. El objetivo era que valiese 0, no es una respuesta mala pero quiza se pueda obtener una mejor de otras formas.

Por ejemplo Wolfram Alpha dice que es

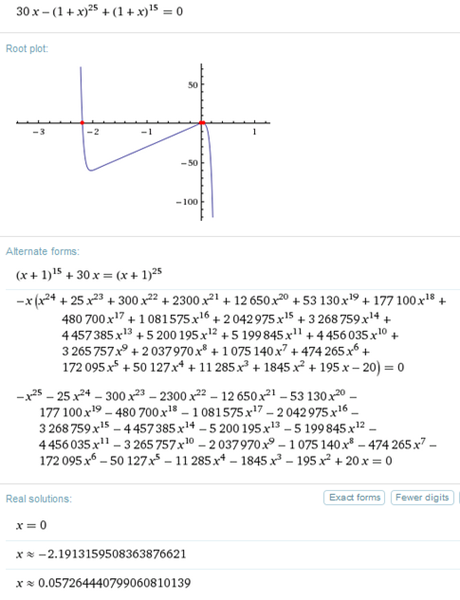
Esta vez escribí la ecuación con x porque con i daba problemas. La que interesa es la tercera, que es la tasa de interés periódico mensual, luego la tasa nominal anual convertible mensualmente es:

12 · 0.05726444 = 0.68717328= 68.72%

:

: