·.·.·.·
·:.:--
¡Hola Oscar!
El motivode no haberlo hecho antes era la pereza de aprender a hacer figuras tridimensionales en Geogebra, pero ya la tengo hecha.
La razón del volumen v1 de la pirámide con respecto al volumen v2 del cubo inscrito en la pirámide, si se sabe que h igual 2a - Matemáticas - Todoexpertos.com
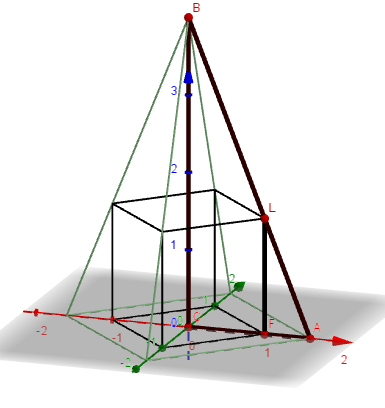
Nuestro objetivo es hallar el lado del cubo LF
Aquí vemos perfectamente que los triángulos ABC y ALF son semejantes.
Luego
$$\begin{align}&\frac{\overline {AB}}{\overline {AL}}=\frac{\overline {BC}}{\overline {LF}}=\frac{\overline{AC}}{\overline{AF}}\\&\\&\text{Creo que la segunda igualdad es más sencilla}\\&\text{llamemos x al segmento }\overline {LF}\\&\\&\frac{h}{x}=\frac{\frac{\sqrt 2 a}{2}}{\frac{\sqrt 2 a}{2}-\frac{\sqrt 2 x}{2}}\\&\\&\frac hx=\frac{a}{a-x}\\&\\&\text{Como }h=2a\\&\\&\frac {2a}x=\frac{a}{a-x}\\&\\&2a^2-2ax=ax\\&\\&2a^2=3ax\\&\\&x= \frac 23a\\&\\&\text{Y ya está}\\&\\&V_1= \frac 13a^2h=\frac 13a^2(2a)= \frac 23a^3\\&\\&V_2= \left(\frac 23 a \right)^3=\frac 8{27}a^3\\&\\&\text{Luego la razon que piden es}\\&\\&\frac{V_1}{V_2}= \frac{ \frac 23a^3}{\frac 8{27}a^3}= \frac{2·27}{3·8}=\frac 94\end{align}$$S a l u d o s.
_=_=_=
-__-_____-

