Los àngulos de elevaciòn de un globo desde dos puntos A y B son 30º y 60º respectivamente.
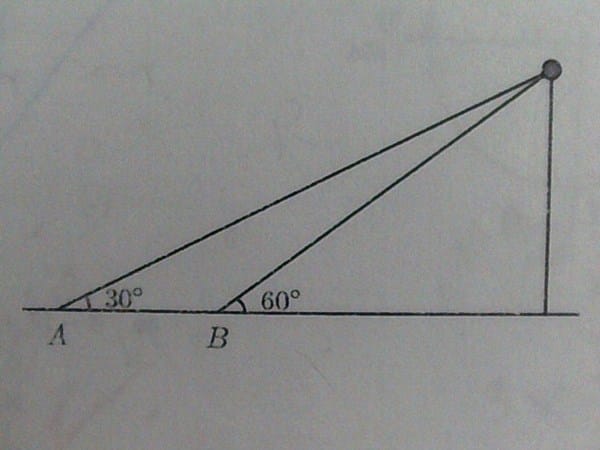
Si la distancia entre estos dos puntos es de 50 m, el globo se halla a una altura de _____________m sobre el suelo.
A. 25 (√3/2)
B. 25/2
C. 25(√3/3)
D. 25/3
2) Se construyò una rampa de 10 metros de altura con una base de 20 metros. El valor del àngulo θ que se le debe incrementar al àngulo α para que la altura de la rampa sea igual a 15 metros, sin cambiar la medida de la base, satisface la siguiente igualdad:
A. Senθ= (11/25)√5
B. Senθ= (11/5)√5
C. Cosθ = (11/25)√5
D. Cosθ = (11/5)√5
Necesito una explicaciòn de como resolver estos ejercicios, gracias.
3 respuestas
Como estas:
Respuesta al ejercicio 1
Colocamos los datos a la figura:
De la figura se observa:
Por lo tanto el triángulo ABC es isósceles, luego AB = BC
2K = 50 m
k = 50 m
Te piden la altura donde se encuentra el globo: CH
Eso es todo, espero que puedas entender. No te olvides de puntuar la respuesta. Si deseas que te resuelva el otro ejercicio mándalo como otra pregunta. Solamente resolvemos un ejercicio por pregunta..
·
·
¡Hola Candy!
La hipotenusa del triángulo inferior por el teorema de Pitágoras será:
$$\begin{align}&h_1= \sqrt{10^2+20^2}= \sqrt{500}=10 \sqrt 5\\&\\&\text{Por lo que}\\&\\&sen\,\alpha= \frac{10}{10 \sqrt 5}= \frac 1{\sqrt 5}\\&\\&\cos \alpha = \sqrt{1- \frac 15}= \frac{2}{\sqrt 5}\\&\\&\\&\\&\text{Y la hipotenusa del triángulo entero es}\\&\\&h=\sqrt{15^2+20^2}=\sqrt{225+400}=\sqrt{625}=25\\&\\&\text{Con ello el seno del ángulo }(\alpha+\theta) \;es\\&\\&sen\,(\alpha+\theta)= \frac{15}{25}=\frac 35\\&\\&\cos (\alpha+\theta)=\sqrt{1-\frac{9}{25}}= \frac{4}{5}\\&\\&\\&\text{Tenemos la fórmula:}\\&\\&sen(a-b)=sena·cosb - cosa·senb\\&\\&\text{que aplicada tendremos}\\&\\&sen \theta =sen((\alpha+\theta)-\alpha)=\\&\\&sen(\alpha+\theta)\cos \alpha-\cos(\alpha+\theta)sen \,\alpha=\\&\\&\frac 35·\frac{2}{\sqrt 5}- \frac{4}{5}·\frac{1}{\sqrt 5}=\frac{6-4}{5 \sqrt 5}=\frac{2}{5 \sqrt 5}=\frac{2 \sqrt 5}{25}\\&\\&\cos \theta= \sqrt{1-\frac{20}{625}}= \frac{\sqrt{605}}{25}=\frac{11 \sqrt 5}{25}\\&\\&\text{Luego la respuesta es la C}\\&\\&\\&\\&\end{align}$$Y eso es todo, saludos.
:
:
El primer dibujo está totalmente desproporcionado y paso a explicar por qué.
Voy a llamar C al punto que queda en la altura del globo y D al que estaría debajo de C
Como ABD es un ángulo llano, y CBD mide 60°, entonces el ángulo ABC mide 120°
El ángulo ACB = 180° - CAB - ABC = 180° - 120° - 30° = 30°
Por lo tanto se el triángulo ABC es isósceles y el segmento BC mide también 50m.
De trigonometría sabemos que
Sen 60° = Opuesto / Hipotenusa
Raiz(3)/2 = Altura / 50
Altura = 25*Raiz(3) (que no la veo entre tus alternativas, salvo que sea la opción D que no está muy clara)
Salu2