Si f( θ)= cos ((pi - θ)/3), entonces f(2pi) - f(0) es igual a:
Hice el ejercicio pero lleguè hasta aquì, no se puede usar calculadora porque es un ejercicio tipo examen de admisiòn, necesito una explicaciòn para llegar a la respuesta, gracias.
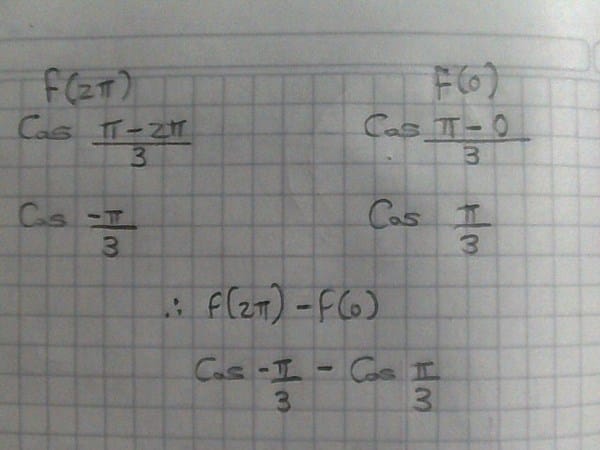
1 respuesta
Respuesta de Valero Angel Serrano Mercadal
2
·
·
¡Hola Candy!
Claro, es un ejercicio para hacer sin calculadora, tienes que evaluar el valor de la función:
$$\begin{align}&f(\theta)=\cos \frac{\pi-\theta}{3}\\&\\&f(2\pi)-f(0)=\cos \frac{\pi-2\pi}{3}-\cos \frac{\pi-0}{3}=\\&\\&\cos \frac{-\pi}{3}-\cos \frac{\pi}3=\\&\\&\text{el coseno de amgulos opuestos es el mismo}\\&\\&\cos \frac{\pi}{3}-\cos \frac{\pi}3=0\\&\\&------------------\\&\\&\text{Si no te das cuenta de eso, tienes que hacer cuentas}\\&\\&\pi\, rad\implies 180º\\&\\&\frac\pi 3 rad\implies 60º\\&\\&=\cos(-60º) - \cos 60º= \frac 12-\frac 12=0\end{align}$$Y eso es todo, saludos.
:
:
Vaya, salio amgulos, es ángulos
