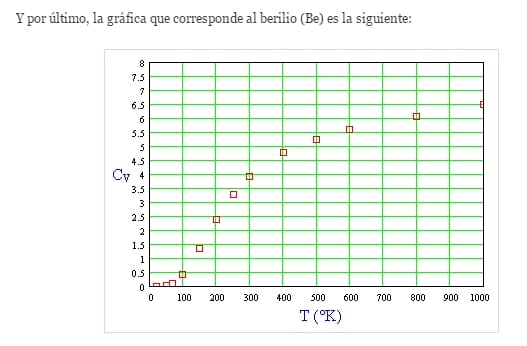
¿Como calculo la capacidad calorífica del Berilio?
Un trozo de Berilio de 500 gramos a una temperatura inicial de 100°C se introduce en un calorimetro que contiene 100 gr de agua a 0°C. Si la Temperatura final de equilibrio térmico es de 70.15°C. Obtenga la capacidad calorífica del Berilio.
2 Respuestas
Respuesta de albert buscapolos Ing°
2
Respuesta de david ..
1