Calcula los ángulos interiores del ∆ ABC
Vectores, Matrices y Determinantes
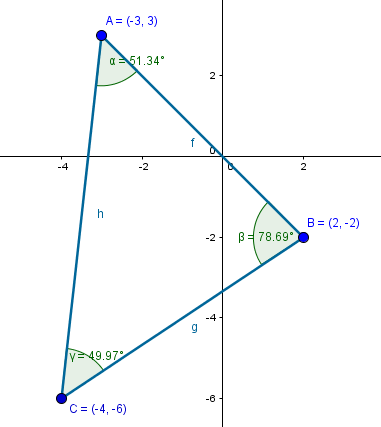
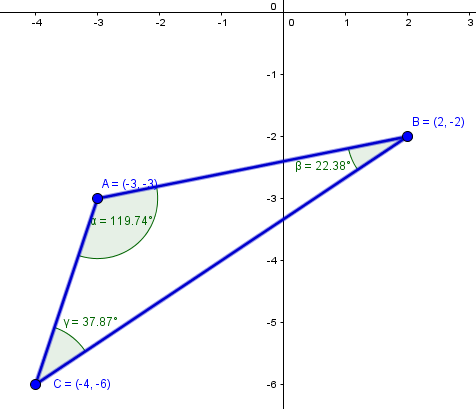
Calcula los ángulos interiores del ∆ ABC con:
A (-3,-3); B (2, -2); C (-4, -6).
Realizar la figura y ver el triángulo formado por los vectores e indicar los ángulos, que se quieren determinar.
2 Respuestas
Respuesta de Valero Angel Serrano Mercadal
1
·
¡Hola Mónica!
Esta es la gráfica:
Para calcular los ángulos necesitaremos los vectores:
$$\begin{align}&\vec{AB}=(2-(-3),-2-3)=(5,-5);\quad\vec{BA}=(-5,5)\\&\vec{AC}=(-4-(-3),-6-3)=(-1,-9);\quad \vec CA=(1,9)\\&\vec{BC}=(-4-2,-6-(-2)=(-6,-4);\quad \vec{CB}=(6,4)\\&\\&\alpha= arc \cos \frac{\vec{AB}·\vec{AC}}{||\vec {AB}||\; ||\vec{AC}||} =arc \cos \frac{(5,-5)·(-1,-9)}{\sqrt{5^2+5^2}\sqrt{1^2+9^2}}=\\&\\&arc \cos \frac{40}{5 \sqrt 2 \sqrt{82}} = arc \cos \frac {4}{\sqrt {41}}= arccos \frac{4 \sqrt{41}}{41}\approx 51.34º\\&\\&\\&\beta=arc \cos \frac{\vec{BA}·\vec{BC}}{||\vec {BA}||\; ||\vec{BC}||}= arc \cos \frac{(-5,5)·(-6,-4)}{\sqrt{5^2+5^2}\sqrt{6^2+4^2}}=\\&\\&arc \cos \frac{10}{5 \sqrt 2·2 \sqrt {13}}= arc \cos \frac{1}{\sqrt {26}}= arc \cos \frac{\sqrt {26}}{26}\approx 78.69º\\&\\&\\&\gamma\approx180º - 51.34º - 78.69º = 49.97º\\&\end{align}$$Y eso es todo, saludos.
:
:
Vaya, me equivoqué con el punto A, lo leí mal y todo está mal. Aquí lo hago de nuevo.
Y estos son los cálculos:
$$\begin{align}&\vec{AB}=(2-(-3),-2-(-3))=(5,1);\quad\vec{BA}=(-5,-1)\\&\vec{AC}=(-4-(-3),-6-(-3))=(-1,-3);\quad \vec CA=(1,3)\\&\vec{BC}=(-4-2,-6-(-2)=(-6,-4);\quad \vec{CB}=(6,4)\\&\\&\alpha= arc \cos \frac{\vec{AB}·\vec{AC}}{||\vec {AB}||\; ||\vec{AC}||} =arc \cos \frac{(5,1)·(-1,-3)}{\sqrt{5^2+1^2}\sqrt{1^2+3^2}}=\\&\\&arc \cos \frac{-8}{\sqrt {26} \sqrt{10}} = arc \cos \frac{-4}{\sqrt{65}}\approx 119.7449º\\&\\&\\&\beta=arc \cos \frac{\vec{BA}·\vec{BC}}{||\vec {BA}||\; ||\vec{BC}||}= arc \cos \frac{(-5,-1)·(-6,-4)}{\sqrt{5^2+1^2}\sqrt{6^2+4^2}}=\\&\\&arc \cos \frac{34}{\sqrt {26}·\sqrt {52}}= arc \cos \frac{17}{13\sqrt {2}}\approx 22.3801º\\&\\&\\&\gamma\approx180º -119.7449º - 22.3801º = 37.8750º\\&\end{align}$$Y eso es todo, perdona por el despiste.
Saludos.
:
:
Respuesta de albert buscapolos Ing°
1
