Problema equilibrio de partícula en el espacio
- Una caja de madera está sostenida en A por tres cables, como se muestra en la figura. Determine la tensión en los cables AB, AC y AD si el peso P de la caja 700 Newton
·
·
¡Hola Christian!
Vamos a calcular las coordenadas de los puntos de acuerdo al sistema de ejes que han puesto, no me gusta porque yo habría puesto z en vertical pero voy a seguir lo que dice el dibujo.
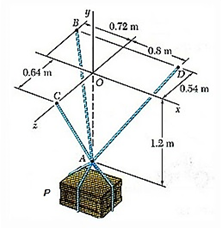
A = (0, -1.2, 0)
B = (-0.72, 0, 0.54)
C = (0, 0, -0.64)
D = (0.8, 0, 0.54)
Y con esto vamos a calcular los vectores
AB = (-0.72, 1.2, 0.54)
AC = (0, 1.2, -0.64)
AD = (0.8, 1.2, 0.54)
Necesitamos los vectores unitarios, para ello hay que dividir las componentes por el módulo del vector. Reutilizaré los mismos nombres para los vectores unitarios. Qué sería de este mundo si no se pudieran reutilizar los nombres de las variables, en el ordenador se hace a todas horas.
||AB|| = raíz(0.72^2 + 1.2^2 + 0.54^2) = 1.5
AB = (-0.48, 0.8, 0.36)
||AC|| = raíz(1.2^2 + 0.64^2) = 1.36
AC = (0, 0.88235294, -0.470588236)
||AD|| = raíz(0.8^2+1.2^2+0.54^2) = 1.54
AD = (0.519480519, 0.779220779, 0.35064935)
Y la suma de las fuerzas por sus vectores debe ser 0
Tb(-0.48, 0.8, 0.36) + Tc((0, 0.88235294, -0.470588236) + Td(0.519480519, 0.779220779, 0.35064935) + (0, -700, 0) = (0,0,0)
Salen estas ecuaciones:
-0.48Tb + 0.519480519Td = 0
0.8Tb + 0.88235294Tc + 0.779220779Td - 700 = 0
0.36Tb - 0.470588236Tc + 0.35064935Td = 0
No es nada divertido resolver estas ecuaciones y no voy a hacerlo a mano, el resultado que da Máxima es este:
Tb=249.7769851678394 N
Tc=363.0508472374864 N
Td=230.7939345085684] N
·
Y eso es todo, saludos.
:
:
Perfecto. Has comenzado planteando los cosenos directores para cada una de las tres rectas de la descomposición. Obviamente el sistema sale complicado para hacerlo manualmente. Sobre todo porque no son coeficientes enteros. Sdos. - albert buscapolos Ing°