·
·
¡Hola Jhon!
A veces los que ponen ejercicios no se dan cuenta de las consecuencias que puede tener lo que escriben.
Faltan algunas premisas implicitas pero que deben ser puestas en la tabla de la verdad ya que si no va a dar resultados incorrectos. Se supone que solo hay un ordenador y solo una tablet, luego que lo gane uno imposibilita que los demos lo hayan obtenido. Asimismo si uno gana el primer premio no gana el segundo y viceversa. Luego sería asi:
a: Ximena gana el ordenador
b: Ximena gana la tablet
c: Johan gana el ordenador
d: Johan gana la tablet
e: Ricardo gana el ordenador
f: Ricardo gana la tablet
g: Carlos gana el ordenador
h: Carlos gana la tablet
Las proposiciones implícitas son:
1) a>(~b & ~c & ~e & ~g)
2) b>(~a & ~d & ~f & ~h)
3) c>(~d & ~a & ~e & ~g)
4) d>(~c & ~b & ~f & ~h)
5) e>(~f & ~a & ~c & ~g)
6) f>(~e & ~b & ~d & ~h)
7) g>(~h & ~a & ~c & ~e)
8) h>(~g & ~b & ~d & ~f)
Y solo ahora vamos con las que nos dan especiales.
9) a > (d+f)
La de "Si Ximena recibió la tablet no obtuvo el ordenador" se deduce de las implícitas.
La de "Si Carlos recibió la tablet Ricardo no recibió la tablet" se deduce de las implícitas.
10) a
Y la conclusión es
11) ~h
Luego la expresión a comprobar va a ser todo esto:
{[a>(~b & ~c & ~e & ~g)] & [b>(~a & ~d & ~f & ~h)] & [c>(~d & ~a & ~e & ~g)] & [d>(~c & ~b & ~f & ~h)] & [e>(~f & ~a & ~c & ~g)] & [f>(~e & ~b & ~d & ~h)] & [g>(~h & ~a & ~c & ~e)] & [h>(~g & ~b & ~d & ~f)] & [a>(d+f)] & a} > ~h
Que ahora vamos a ver si es capaz de soportar el programilla ese.
·
Como suponía, vaya birria de programilla, solo admite expresiones de pocos caracteres
Emtonces vamos a tener que trabajar solo con las que nos dan explicitamente y luego con las implícitas por nuestra cuenta. Al usar solo las explicitas ni siquiera se presentarán todas las proposiciones simples
1) a>(d+f)
2) a
Y la conclusión
3) ~ h
Luego comprobamos
{[a>(d+f)] & a}>~h
Y la tabla es esta:
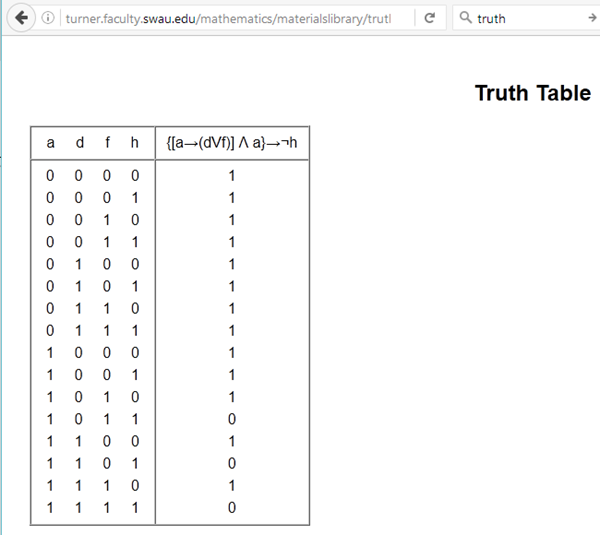
Pero ahora debemos comprobar si las tres que han dado fallo cumplían las restricciones implícitas o no.
Tenemos la primera donde son verdaderas a, f, h. No puede ser porque la restricción 6 dice f>(~e & ~b & ~d & ~h), luego si f es verdadera h es falsa, no hay dos que puedan ganar la tablet.
La segunda que ha dado fallo dice que son verdaderas a, d, h. Incumple alguna, no voy a mirar cuál es, simplemente fíjate que hay tres verdaderos, entonces ya sea el ordenador o la tablet ha sido ganado por dos personas, lo cual incumple las normas que di.
Y en la tercera que falla son verdaderas a, d, f, h. Pero me lo pones ha habido cuatro ganadores para dos premios.
Y todas las demás son verdaderas, aun cuando habrá algunas que tampoco podrán darse por superar los dos ganadores. Las que no lleguen a dos ganadores pueden ser que valgan porque no fueron presentadas las 8 proposiciones simples.
En conclusión, el razonamiento es válido.
Ni que decir tiene que sería muy posible que el profesor no esté de acuerdo conmigo, es lo que tiene poner ejercicios donde no se han medido las consecuencias.
Y eso es todo, sa lu dos.
:
:




