Matrices dada la matriz A y B ¿Es la matriz C inversible?
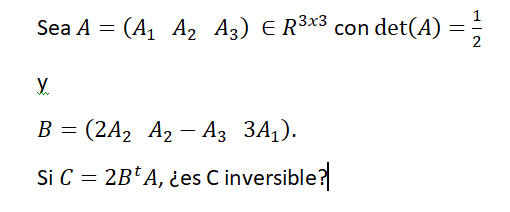
¿Hola gente me ayudan con este ejercicio? Es de Álgebra y me esta costando mucho.
2 respuestas
;)
Hola Leonardo Montalto!
Una matriz es invertible si su determinante es diferente de 0.
Todo se basa en aplicar las propiedades de los determinantes
detC=|C|=|2B^t·A|=2^3·|B^t|·|A|=8·|B|·|A|=4·|B|=4 |2A_2 ,A_2-A_3 , 3A_1|=
Propiedades
Factor común al 2 en una matriz 3X3 (a cada fila)=> 2^3
det (AB)=detA·det B
detB^t=detB
desglose de la segunda columna: el primer determinante da 0
4|2A_2 , A_2 , 3A_1 | + 4 |2A_2 , -A_3 , 3A_1 |= 0 + 4(2)(-1)(3) |A_2 , A_3 , A_1 |=
dos lineas múltiples (2A_2 y A_2) => 0
factor común a 2, -1, y 3
=-24 |A_2,A_3 , A_1| = -24 |A_1, A_2,A_3 |= -24·1/2 = -12
dos trasposiciones ==> el determinante no varia
Como eldeterminante da diferente de 0, C es inversible
Saludos!!
https://www.matematicasonline.es/BachilleratoCCNN/Segundo/formulas/determinantes-propiedades.pdf
||*||
;)
Podemos aprovechar que este determinante es una función trilineal alternante
$$\det(B^t)=
\left|\begin{matrix}
2A_2\\
A_2-A_3\\
3A_1
\end{matrix}\right| =
(2\times 3)\left|\begin{matrix}
A_2\\
A_2-A_3\\
A_1
\end{matrix}\right| =
6\left|\begin{matrix}
A_2\\
-A_3\\
A_1
\end{matrix}\right| =
-6\left|\begin{matrix}
A_2\\
A_3\\
A_1
\end{matrix}\right| =
6\left|\begin{matrix}
A_2\\
A_1\\
A_3
\end{matrix}\right| =
-6\left|\begin{matrix}
A_1\\
A_2\\
A_3
\end{matrix}\right|=-3$$Hallemos el determinante de C
$$\begin{align}&\det(C) = \det(2B^t\cdot A)=2\det(B^t)\cdot \det(A)=2\cdot -3\cdot\frac{1}{2}=-3\neq 0\end{align}$$Como el determinante de C es no nulo entonces C es invertible
Fe de errata: en la última parte en det (C), en lugar de 2, debió ser 2^3 = 8