Cónicas y Cuadricas ¿Hallar A, B, C para que la superficie sea un cilindro circular recto?

:)
Hola Leonardo!
Para que sea un cilindro recto, con eje paralelo al eje z, ya que la proyección en z=-2 ( que será la misma que en z=0) es una circunferencia, lo primero que tiene que cumplirse es C=0.

Ya que si A, B y C son distintos de 0, tendríamos una esfera

Luego

$$\begin{align}&A(x-2)^2+B(y+3)^2=1\end{align}$$

La circunferencia tendrá centro en (2,-3,-2)

Las circunferencias en el plano XY tienen de ecuación:

$$\begin{align}&(x-a)^2+(y-b)^2=r^2\\&\\&Luego \ la \ proyección \ tendrá \ de \ equación\\&(x-2)^2+(y+3)^2=3^2\end{align}$$

Observa que para que sea una circunferencia, y no una elipse , A=B

Luego para obtener lo deseado A=B= 1/9

$$\begin{align}&\frac 1 9 (x-2)^2+ \frac 1 9 (y+3)^2=1\\&\\&(x-2)^2+(y+3)^2=9=3^2\\&\\&A= B= \frac 1 9\\&\\&C=0\end{align}$$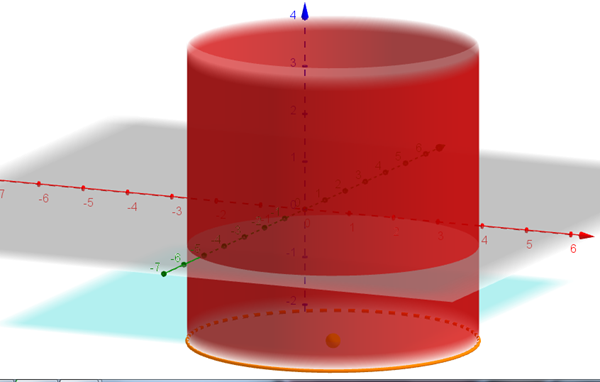

Saludos y recuerda votar

;)

;) 

;)
Esfera :

$$\begin{align}&(x-2)^2+(y+3)^2+z^2=25\\&Si\\&A=B=C\\&esfera\ de \ centro \ (2,-3,0)\ y \ radio \ 5\\&\\&Si\\&A \neq B\neq C \\&es \ un \ elipsoide\\&4x^2+3y^2+z^2=1\\&Elipsoide \ de \ centroº (0,0,0)\end{align}$$

;)

;)
Superficie cilíndrica:

$$\begin{align}&(x-a)^2+(y-b)^2= r^2\end{align}$$

Saludos

;)

;)