Cual es la frecuencia de resonancia de un volante de inercia?
El volante de inercia es un elemento pasivo dentro de un sistema mecánico que almacena energía cinética y se sigue moviendo hasta que pierde esta energía. ¿Se podría hallar la frecuencia de resonancia de un volante de inercia?
El volante para de girar porque gasta su energía cinética en forma de calor (rozamiento), ya sea contra la carga, el aire o los rodamientos.
La "frecuencia de resonancia", tendría que ver con el DESEQUILIBRIO que tenga ese volante. Si es "perfectamente equilibrado"... no vibra: O lo que es más o menos lo mismo, la "frecuencia de resonancia" seria cero.
Por lo tanto, no le veo demasiado sentido a tu pregunta.
Por favor me corriges si estoy equivocado. Un volante de inercia gira porque se le aplica algún tipo de energía fuerza, movimiento, velocidad) esta energía se acumula o se almacena hasta que se gasta en forma de calor por fricción con el aire. No es posible mantener la energía aplicada si se le suministra a determinada frecuencia (frecuencia de resonancia) para mantener conste su movimiento aplicando determinada fuerza. Gracias por la ayuda y orientación
Si, es posible... pero vamos a profundizar un poco mas el tema:
El volante, si fuese todo "ideal", giraria para siempre. Los distintos rozamientos, hacen que la velocidad decaiga con una curva exponencial (aproximada... porque si uno "hila fino" habra distintas cargas con distintas formas de accion que intentan detenerlo).
Si yo le aplico una fuerza cada tantos segundos, hasta llevarlo a la "velocidad de regimen", si, se mantendra mientras siga aplicando esos "pulsos de fuerza". Pero fijate que ese "pulso de fuerza" le provoca una aceleracion para llevarlo a la "velocidad de regimen: Asi que su "Velocidad angular" sera una curva periodica de las que llamamos "Diente de sierra exponencial", montada sobre una "Velocidad media constante".
El dibujo que encontre es electrico, pero la ecuacion si uno la desarrolla, es exactamente igual:
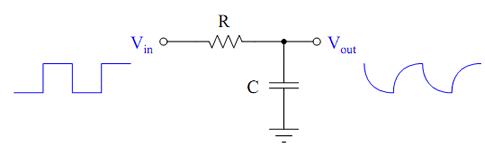
Ahora bien: No existe una "Unica frecuencia" donde un pulso pueda mantener ese valor: Lo que habra es toda una "familia de pulsos", donde mientras guarde determinada relacion entre EL ANCHO Y EL ALTO DEL PULSO (Duracion en segundos sobre fuerza ejercida), la velocidad del volante se mantendra.
O sea que: Si tengo determinada fuerza para aplicar, debere calcular "el ancho del tiempo que la aplico", o viceversa; si "deseo aplicar un pulso de tantos segundos", debere calcular el modulo de la fuerza a aplicar.
Y la fuerza debera ser, o bien tangencial al borde del volante, o bien rotacional sobre el eje..
La rotacional sobre el eje, podria consistir en "Encender el motor que lo impulso durante un segundo cada 20 segundos", como para dar un ejemplo practico.
¿Esta mas claro ahora?
Tal vez wilton estaba confundiendo frecuencia de resonancia con inercia rotacional del volante. Son conceptos distintos. - albert buscapolos Ing°
No, creo que pensaba que la frecuencia para lograrlo eres "solamente una", no que podría ser una gama infinitamente amplia, dependiendo de la precisión con que se quiera mantener la velocidad. Digamos "Problema de Control Automático". - Boris Berkov