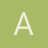Matrices y determinantes, aplicando propiedades encontrar el valor del siguiente determinante.
Hola gente de todo expertos, por favor me ayudan con este ejercicios, que no logro resolver.
1 respuesta
Respuesta de Andrés L.
2
Las propiedades que usaremos son:
El determinante de la traspuesta es igual:
$$\begin{align}&|B^t|=|B|\end{align}$$El determinante de la inversa es el inverso del determinante:
$$\begin{align}&|B^{-1}| = |B|^{-1}\end{align}$$El determinante del producto es el producto de los determinantes:
$$\begin{align}&|A\cdot B| = |A|\cdot |B|\end{align}$$El determinante de una matriz por un escalar es el determinante de la matriz multiplicado por el escalar elevado a la dimensión de la matriz. Si la matriz B es cuadrada de dimensión 3, entonces
$$\begin{align}&|2\cdot B|=2^3\cdot|B|\end{align}$$Vamos allá:
El primer sumando es
$$\begin{align}&|2B^{-1}A|=|2B^-1||A|=\\&=2^3|B^{-1}||A|=8·|B|·|A|=\\&=8·(-1)·5=-40\\&\end{align}$$El segundo sumando es
$$\begin{align}&|A^2B^t|=|A^2||B^t|=\\&=|A^2||B|=|A||A||B|=\\&=5^2·(-1)=-25\end{align}$$Por tanto, el resultado es
$$\begin{align}&-40-(-25)=-40+25=-15\end{align}$$Las propiedades las puedes comprobar en Determinante, rango y menores (teoría).
Un saludo, amigo. Te dejo unos enlaces de problemas de álgebra matricial:
