¿Cuál es la solución de este problema de geometría analítica?
Un punto C equidista de los puntos A(4,5) y B(-2,-3). Si el área del triángulo ABC es 10u^2.Calcular coordenadas de C.
3 Respuestas
Primero vamos a designar como "b" la recta AB; como "c" la recta BC y como "a" la recta AC.
Como solo tenemos 2 puntos, tomemos la recta AB como la base del triangulo a calcular. Entonces tenemos que conocer la longitud de la recta AB:
$$\begin{align}&Longitud AB=\sqrt {(X_B-X_A)^2+(Y_B-Y_A)^2}\\&AB=\sqrt {(-2-4)^2+(-3-5)^2 }\\&AB=\sqrt {36+64}=\sqrt {100}=10\\&\end{align}$$Con este valor como base, calculamos la altura del triangulo usando la formula del area, donde se sustituyen los valores conocidos para despejar "h".
$$\begin{align}&A_{rea}=\frac {b×h}{2}\\&10=\frac {10×h}{2}\\&20=10h\\&h=2\\&\end{align}$$Luego la altura es de 2 unidades. Siendo la altura una recta perpendicular a la base en el punto medio de esta, podemos formar un triangulo rectangulo con la mitad de la base, la altura y el lado "c".
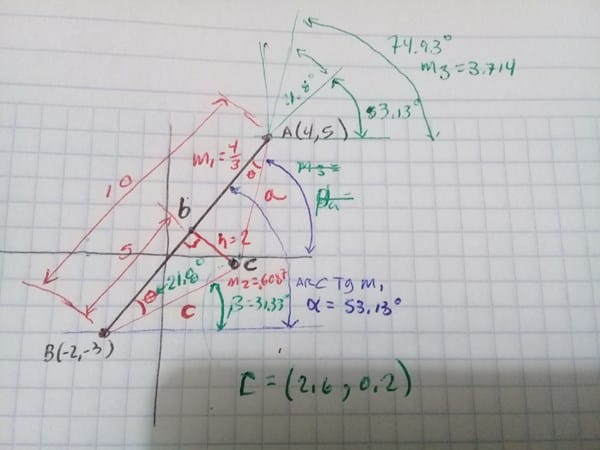
Ojala la imagen no te resulte confusa. Puedes identificar el triangulo que recién formamos.
Este triangulo lo queremos para calcular el angulo theta del triangulo. Usando la función tangente:
$$\begin{align}&{\theta}=arctg\frac {h}{\frac {b}{2}}\\&{\theta}=arctg\frac {2}{5}=21.8°\\&\end{align}$$El proposito de calcular este angulo, es calcular la pendiente de el lado "c". Para eso, primero calculamos la pendiente de la base (m1), y con ella el angulo de la base con el eje "X" (afa) , le restamos el valor del angulo theta y encontramos cuanto vale el angulo del lado "c" (beta), para luego calcular su pendiente (m2):
$$\begin{align}&\\&m_{1}=\frac {Y_B-Y_A}{X_B-X_A}\\&m_{1}=\frac {-3-5}{-2-4} \\&m_{1}=\frac {-8}{-6}=\frac {4 }{3}\\&\\&{\alpha}=arctg\frac{4}{3}=53.13°\\&\\&{\beta}={\alpha}-{\theta}\\&{\beta}=53.13-21.8=31.33°\\&\\&m_2=tg31.33=0.6087\\&\end{align}$$Con la pendiente y el punto "B", podemos desarrollar la ecuacion de la recta del lado "c".
$$\begin{align}&Y_b=m_2X_b+b_c\\&-3=0.6087 (-2)+b_c\\&-3=-1.217+b_c\\&b_c=-3+1.217=-1.782\\&\end{align}$$Luegonla ecuacion del lado "c" es:
C) Y=0.6087X-1.782
Ahora vamos a utilizar un procedimiento parecido para encontrar la ecuación de la recta del lado "a".
Para lo cual observamos en el punto "A" que el angulo del lado "a" con el eje "X", es igual al angulo beta más el angulo interno del punto "A" que es igual al angulo theta. Y utilizamos este resultado para calcular el angulo del lado "a" y conocer así su pendiente m3, con lo que deducimos la ecuación de la recta que fora el lado "a".
$$\begin{align}&{\gamma}={\alpha}+{\theta}\\&{\gamma}=53.13 + 21.8=74.93°\\&\\&m_3=tg 74.93°=3.714\\&\\&Y_A=m_3X_A+b_a\\&\\&5=3.714 (4)+b_a\\&5-14.856=b_a\\&b_a=-9.856\\&\\&\end{align}$$Luego la ecuacion para el lado "a" es:
A) Y=3.714X-9.856
Para que todo este rollo de calcular las ecuaciones de los lados "a" y "c"?
Bueno, porque las dos rectas tienen un punto común que es el punto "c". Eso significa que:
$$\begin{align}&Y_c=Y_a\\& \\&0.6087X-1.782=3.714X-9.856\\&-1.782+9.856=3.714X-0.6087X\\&8.074=(3.714-0.6087)X\\&X=\frac {8.074}{3.2053}=2.6\end{align}$$Y ya tenemos el valor de "X", el cual sustituimos en C) para encontrar el valor de "Y":
$$\begin{align}&Y=0.6087X-1.782\\&Y=0.6087 (2.6)-1.782\\& Y=0.199\\&\end{align}$$Y ahi esta, podriamos decirbque Y=0.2.
Por lo que las coordenadas del punto "C" son:
(2.6, 0.2). Y he aquí resuelta la mitad del problema.
¿Por qué solo la mitad? Pues porque la altura "h" resulto de una raíz cuadrada, lo que significa que puede tener valores de 2 y -2, es decir, que hay otro punto, que cumple con los postulados del enunciado. Por lo que el vértice "C" puede también estar del lado opuesto de la recta que tomamos como base.
Te toca a ti, encontrar las coordenadas del otro punto.
Sigue esta metodología.
Tenemos A(4,5) y B(-2,-3), es fácil hallar la medida del segmento AB = 10, sea
$$\begin{align}&d(C,\overline{AB})=h\end{align}$$la distancia de C al segmento AB. sabemos el área del triángulo ABC
$$\begin{align}&[ABC]=\frac{h\times \overline{AB}}{2}\\&\\&10 = \frac{h\times 10}{2}\\&\\&\boxed{h=2}\end{align}$$Hallemos los vectores unitarios ortogonales al vector AB, sabiendo que
$$\begin{align}&\vec{u}_{AB}=\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}=\frac{(-6,-8)}{10}=\frac{1}{5}(-3,-4)\\&\\&\text{Por ende:}\\&\\&\vec{u}^{\bot}_1=\frac{1}{5}(4,-3)\\&\\&\vec{u}^{\bot}_2=\frac{1}{5}(-4,3)\\&\\&\end{align}$$Como C equidista de ambos puntos, el triangulo ABC es isósceles. Sea M=(1,1) el punto medio entre A y B, entonces C se halla así
$$\begin{align}&C= M +h\cdot \vec{u}^{\bot}_1\\&\\&ó\\&\\&C= M +h\cdot \vec{u}^{\bot}_2\\&\\&============\\&\\&C= (1,1)+2\cdot \frac{1}{5}(4,-3)=\left(\frac{13}{5},-\frac{1}{5}\right)\\&\\&ó\\&\\&C=(1,1)+2\cdot \frac{1}{5}(-4,3)=\left(-\frac{3}{5},\frac{11}{5}\right)\end{align}$$