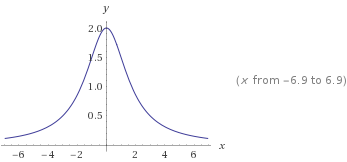
Determinar los intervalos de concavidad y los puntos de inflexión [si es que existen]de la siguientefunción: ℎ(?) =

A. Determina la segunda derivada de ℎ(?)

h' (t) = -12 t / (t^2 + 3)^2 .........................se anula para t= 0

h'' (t) = dh' / dt= 36 (t^2 - 1) / (t^2 + 3)^3

B. Resuelve la ecuación ℎ(?) = 0 y determina sus raíces.

h(t) = 0 no tiene raices reales. Tiende a 0 para t tendiendo a +/- infinito.

C. Escribe los intervalos de concavidad.

Anulando la 1er. derivada tenes:

 -12 t / (t^2 + 3)^2 = 0  ..............t1 = 0 ......t2= t3 = +/- infinito.

D)Determina y escribe los puntos de inflexión [si es que existen]. Caso contrario, explicar por qué no existen dichos puntos.

Anulando la derivada 2da. tendrias ....36 (t^2 - 1) / (t^2 + 3)^3 = 0 .........que se anula para t = +/- 1....Esos serian los dos puntos de inflexion.