Teorema del valor medio para demostrar
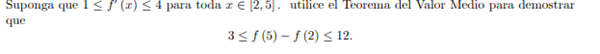
me orientan por favor ocmo realizar esta demostracion en el intervalo [2,5]
1 respuesta
Respuesta de Alejandro Salazar
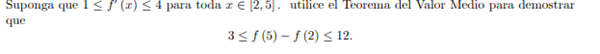
me orientan por favor ocmo realizar esta demostracion en el intervalo [2,5]

No entiendo la relación del segundo ejemplo con con la demostración que pide el enunciado ,seria de gran ayuda si me explicaras - Andrea perez
No hay problema. El primer recuadro muestra lo que nos dice el teorema del valor medio, que en palabras significa que si eliges un intervalo, y la función es continua en ese intervalo. Lo que puedes hacer es con una línea unir los dos extremos y lo que nos dice el teorema es que existe un punto(lo llamaremos c) en ese intervalo cuya pendiente de la recta tangente es igual a la pendiente de esa línea que trazamos, que coincide recordando conceptos con la derivada en ese punto.El enunciado dice que para toda x en el intervalo [2,5] se cumple que 1< f'(x)< 4. Y ya que c pertenece al intervalo, tambien debe cumplir esa desigualdad 1<f'(c)<4. - Alejandro Salazar
Pero por el teorema del valor medio, sustituyendo los extremos por sus valores numéricos tenemos1<(f(5)-f(2))/(5-2)< 4. Yo no sustitui los extremos, deje que la persona lo hiciera. Pero a partir de ahí, 5-2 = 3, y multiplicando la desigualdad nos queda en 3<f(5)-f(2)<12 - Alejandro Salazar