Como podría hallar el rango de la siguiente función irracional
$$\begin{align}&f(x)=3-\sqrt{15-2x-x^2}\end{align}$$me podrían ayudar con la siguiente función irracional para que la respuesta sea:
$$\begin{align}&x ∈ R¬ {-1/2} \\&\\&y\ge -2\end{align}$$donde X pertenece a todos los reales excepto el {-1/2}
Donde Y es mayor o igual que -2
1 respuesta
Rango es el conjunto de valores que puede tomar la función recorriendo todo el eje real x.
f(x) = 3 - V(15 - 2x - x^2)
Dado que la raíz solo admite radicandos >= 0, fíjate de entrada que desarrollando el radicando:
15 - 2x - x^2 es una parabola concava hacia abajo, con raices reales = 2 +/- V ( 4 +60) / (-2)
= {2 +/- 8} / - 2 ...............x1 = - 5...........x2 = 3
Luego el dominio valido serán los -5 <= x <= 3
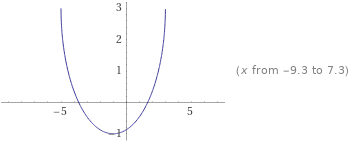
La función completa que te están dando = 3 - V(15 - 2x - x^2) será entonces una parábola invertida ( por el -) cóncava hacia arriba.
El rango seran los valores de y(x) que puede tomar entre los -5 <= x <= 3 incluidos.
Para x= -5 ..............la funcion toma el valor {3 - V(15 + 10 - 25)} = 3.
Para x= 3 ............. la funcion toma el valor {3 - V(15 -6 - 9)} = 3.
El vertice de la parabola será = -b/ 2a = 2/(-2) = - 1
Luego el rango de la misma será el conjunto de "y " comprendido entre el minimo = -1 y el maximo = +3 incluidos.
No se entiende el significado de los valores que estas indicando como resultados al final.
