Fuerza que impulsa carga en su trayectoria
Cuando se se calcula el trabajo realizado por una carga eléctrica puntual normalmente se acude a un dibujo muy parecido a este donde el vector dr, se pone como el vector dl por cos a (angulo entre dl y dr), es decir :
Vector dr= dl * cos (a), y luego se sigue con la integral hasta llegar al final de la fórmula
We(A→B)=−K⋅Q⋅q⋅[1/rB−1/rA]
Mi pregunta es buscar el sentido físico a la sustitución de dr por dl. Cos(a).
Me explico: Si la fuerza eléctrica va radialmente desde Q (carga fuente), nunca jamás podrá realizar desplazamiento de la carga que no sea radialmente, por lo tanto la trayectoria que se dibuja de A hasta B es ficticia ya que si la fuerza eléctrica mueve la carga q lo hará siempre empujándola radialmente y nunca la desplazará en el sentido de la trayectoria dibujada.
Pregunta: ¿Por qué se dibuja esa trayectoria -u otra parecida- para deducir el trabajo realizado sobre una carga puntual q en un campo creado por una carga Q?, ¿Y si se dibuja así qué fuerza es la responsable del movimiento hacia B desde A de la carga q?.
Para complementar la información que ha dado Albert. Recuerda que si bien es cierto que una carga puntual producirá unas líneas de campo radiales. En general habrás muchas cargas, no puntuales además, pero que simplificando podemos considerarlas como tal y por tanto el campo neto es mucho más complejo que algo radial, y con ello la trayectoria que sigue. En la página web te muestran el trabajo que realiza la fuerza que genera el campo producido por 1 sola carga
Gracias.
Entonces, ¿debo entender que en el ejemplo de la página web la trayectoria dibujada es incorrecta para ese caso concreto del campo que genera una sola carga?
Disculpa la tardanza, no me había llegado una notificación. Efectivamente, lo que pasa es que cuándo calculas el trabajo realizada por una fuerza, te quedas con la trayectoria y te olvidas de las otras fuerzas. En el dibujo que muestran pues hacen eso implícitamente
1 respuesta más de otro experto
El tema pasa porque el campo eléctrico es un campo conservativo y la carga que decís seguirá la línea de campo correspondiente. Pero las líneas no son todas (radiales) como decís, luego la trayectoria elemental de la carga será tangente a la línea de campo, y a esa distancia la llaman dl. La distancia del recorrido elemental real entre cargas la llaman dr. Y el angulo entre estos diferenciales seria el a . El trabajo elemental para ese desplazamiento es precisamente dW = /dF/ x /ds/ x cos a . El desarrollo de la integral al final del articulo te lo muestra claramente.
Las líneas de campo que salen de la moneda cargada (+) no son todas directas. Dependiendo del punto donde este la carga será el angulo entre la línea de campo y la distancia entre la carga puntual y el centro de la moneda cargada. Si la carga siguiese la trayectoria del centro, el angulo a = 0.
Gracias por responder.
Lo que comenta es completamente cierto, sin embargo lo que no comprendo es porque se utiliza este dibujo https://www.fisicalab.com/apartado/trabajo-electrico
para indicar una trayectoria general de la carga q en el campo creado por la carga fuente Q, cuando esa carga fuente Q concreta de ese dibujo solo emite líneas directas (desde ella misma como fuente siempre radialmente hacia fuera). Esa trayectoria general (curvilínea de A a B) dibujada nunca se daría si soltásemos la carga de prueba positiva q en el campo generado por Q. Si esa trayectoria fuera correcta, ¿de donde sale la fuerza para desplazar la carga hacia el sentido donde el ángulo "a" NO fuera CERO.?. Es decir la fuerza para desplazar la carga para que vaya recorriendo la trayectoria dibujada nunca podría ser la fuerza eléctrica ya que esta es siempre radial y nunca en otro sentido.
Si.te entiendo perfectamente. Yo trataba de explicarte de donde salia el angulo "a". Siendo aqui una sola carga espacial todas las lineas son radiales, como bien decis, y luego el trabajo W = Fuerza x Distancia, ambos vectores colineales.
W varia con la distancia porque el Campo Eléctrico crece a medida que nos acercamos a la carga fija mientras la distancia disminuye. De allí la integral.
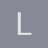
Así es Alejandro. Siendo una carga única en el espacio las líneas serán radiales y el angulo a =0. Pero yo trate de aclararle por que interviene ese angulo en la expresión del trabajo dentro de una campo electrostático. Me parece que no le aclare´mucho... Sdos. - albert buscapolos Ing°