Ayuda con dinámica!
Espero puedas ayudarme, lo más pronto posible... Mi puntuación sera excelente...
4. Una masa de 1kg que esta sujeta al extremo de una cuerda se mueve en una circunferencia vertical de radio R=2m como se muestra en la figura. Si en punto P la tensión en la cuerda es 45N. En ese instante determinar:
a) El vector velocidad.
b) Las componentes tangencial y radial de la aceleración.
c)La magnitud de la fuerza total que actúa sobre la masa.
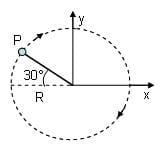
4. Una masa de 1kg que esta sujeta al extremo de una cuerda se mueve en una circunferencia vertical de radio R=2m como se muestra en la figura. Si en punto P la tensión en la cuerda es 45N. En ese instante determinar:
a) El vector velocidad.
b) Las componentes tangencial y radial de la aceleración.
c)La magnitud de la fuerza total que actúa sobre la masa.
2 respuestas
Respuesta
1
a) Realizando una descomposición de fuerzas según los ejes tangencial y normal a la trayectoria tendremos:
V = raíz[R·(T+mgsen(alfa))/m] = 10 m/s
El vector velocidad será: V = VCos(90-alfa) i + VSen(90-alfa) j = 5 i + 8,66 j (m/s)
b) La componente radial es igual a la aceleración centrípeta: ar = ac = 50 m/s^2
La componente tangencial es debida al peso: at = gcos(alfa) = 8,49 m/s^2
c) F = m·raíz(T^2·cos^2(alfa)+(g^2+T^2·sen^2(alfa))= 50,62 N
Un saludo, Vitolinux
V = raíz[R·(T+mgsen(alfa))/m] = 10 m/s
El vector velocidad será: V = VCos(90-alfa) i + VSen(90-alfa) j = 5 i + 8,66 j (m/s)
b) La componente radial es igual a la aceleración centrípeta: ar = ac = 50 m/s^2
La componente tangencial es debida al peso: at = gcos(alfa) = 8,49 m/s^2
c) F = m·raíz(T^2·cos^2(alfa)+(g^2+T^2·sen^2(alfa))= 50,62 N
Un saludo, Vitolinux
Respuesta de leviatanxxi
1
Disculpa la tardanza; He estado ocupado.
Trazamos un sistema cartesiano centrado en P, de forma que el eje "j" coincida con la dirección de la cuerda.
En el eje "j" tenemos las siguientes fuerzas:
Fcentrípeta (hacia fuera), T(hacia dentro), componente j del Peso (hacia dentro). Por tanto:
Fc = Pj + T
m·v^2/r = m·g·cos30 + T
Despejando obtenemos el módulo del vector velocidad: v = 10.34 m/s. La dirección y sentido serían los del movimiento del objeto.
La componente radial de la aceleración (aceleración centrípeta) es: ac = v^2/r = 10.34^2 / 2 = 53.46 m/s^2.
La componente tangencial la sacamos de observar la fuerza responsable del movimiento. En el eje "i" (eje en el que se produce el movimiento) solo actú ala componente "i" del peso, luego:
Ftotal = Pi = m·g·sen30 = 1·9.8·sen30 = 4.9 m/s^2
Como según 2ª ley de Newton Ftotal = m · a, despejamos para obtener aceleración tangencial: a = 4.9 m/s^2
Trazamos un sistema cartesiano centrado en P, de forma que el eje "j" coincida con la dirección de la cuerda.
En el eje "j" tenemos las siguientes fuerzas:
Fcentrípeta (hacia fuera), T(hacia dentro), componente j del Peso (hacia dentro). Por tanto:
Fc = Pj + T
m·v^2/r = m·g·cos30 + T
Despejando obtenemos el módulo del vector velocidad: v = 10.34 m/s. La dirección y sentido serían los del movimiento del objeto.
La componente radial de la aceleración (aceleración centrípeta) es: ac = v^2/r = 10.34^2 / 2 = 53.46 m/s^2.
La componente tangencial la sacamos de observar la fuerza responsable del movimiento. En el eje "i" (eje en el que se produce el movimiento) solo actú ala componente "i" del peso, luego:
Ftotal = Pi = m·g·sen30 = 1·9.8·sen30 = 4.9 m/s^2
Como según 2ª ley de Newton Ftotal = m · a, despejamos para obtener aceleración tangencial: a = 4.9 m/s^2