Cuanta energía mecánica tiene al principio en su punto mas alto

Pues mira, si se "deja caer" supongo que su velocidad inicial es nula Vo=0 m/s. 

Supongo que nos encontramos en la superficie terrestre, donde la intensidad del campo gravitatorio para la variación distancias (5 metros) se puede aproximar, con un error muy pequeño, a un campo de intensidad constante G=9.8 m/s^2.

Nos encontramos en dos situaciones ahora: 1- si consideramos que el cuerpo de masa 2Kg tiene dimensiones ( las cuales no detallas en el enunciado ) entonces la fuerza de rozamiento del aire sería la siguiente:

F = -kv²
Donde es que= fkWS, siendo (sistema MKS):
f: factor de forma. Para una superficie plana, f= 1, para una esfera, f = 1/2.
KW: Constante de resistencia unitaria del aire. kW =0,6 N×s2/m4
S:Superficie frontal que se opone al aire. Para un círculo, S = pD²/4

Pero como no me das las dimensiones del cuerpo voy a tener que suponer que nos encontramos ante una masa puntual (que no tiene dimensiones), y a consecuencia de esto, la resistencia del aire en oposición del movimiento no tendrá sentido.

Siguiendo con el problema, la ecuación del movimiento es la siguiente:

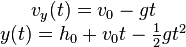
Y teniendo conocido ya el estado del sistema, la pregunta es cual es su energía mecánica en el instante inicial. Sabiendo que la energía mecánica es la energía que se debe a la posición y al movimiento de un cuerpo, por lo tanto, es la suma de las energías potencial y cinética de la masa puntual.

Nos encontramos con que la masa tiene velocidad nula inicialmente con lo que su energía cinética también será nula, y su energía mecánica será igual a su energía potencial.

Como la única fuerza que actúa sobre la masa puntual es la fuerza gravitatoria, su energía potencial será el potencial asociado al campo gravitatorio. Y como hemos supuesto el campo gravitatorio uniforme su energía potencial tiene la siguiente expresión.

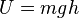
De lo cual sacamos que la energía mecánica Em=5mg.

Y por último, si pierde energía en el rebote nos encontramos ante un choque inelástico o perfectamente inelástico, con lo cual el trabajo interno es menor que 0. Lo que quiere decir en este caso es que el módulo de la velocidad antes del choque es mayor que el de después del choque, siendo el caso extremo en el que la masa puntual queda pegada al suelo.
Esto se expresa de la siguiente manera:

-e(u1-u2)=v1-v2

Donde e es el coeficiente de restitución, u1 y u2 las velocidades de la partícula y del suelo antes del choque, y v1 y v2 las velocidades de la partícula y del suelo después del choque. En este caso tenemos que u2 y v2 es 0 o se podría decir "casi 0" ya que la masa de la tierra en comparación con la de la masa puntual es mucho mayor.