El volumen generado en la rotación del área comprendido por las funciones

He aquí el dibujo imprescindible para entenderlo. En azul están dibujados los ejes respecto a los que girará y el área que generará el volumen al rotar.

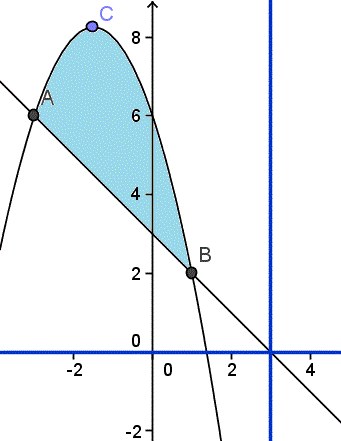
Calculamos los puntos A, B y C.

y = -x^2 - 3x + 6

y = 3-x

-x^2 - 3x + 6 = 3-x

x^2 + 2x - 3 = 0

xa=-3; xb= 1

A=(-3, 6)

B=(1,2)

C es el vértice de la parábola

xc= -b/2a = 3/(-2) = -3/2

yc= -9/4 + 9/2 + 6 = 6+9/4 = 33/4

C=(-3/2, 33/4)

b)

Hago primero la parte b que es más fácil.

Gira en torno al eje X, se usa la fórmula tal cual. Al volumen generado por la parábola restaremos el generado por la recta. Los límites de las funciones son x=-3 y x =1. Aprovecharemos la misma integral, pero ojo el cuadrado afecta a cada función por separado, no sirve restar las funciones y luego elevar.

$$\begin{align}&V= \pi \int_{-3}^1[(-x^2-3x+6)^2-(3-x)^2]dx=\\ &\\ &\\ &\\ &\pi \int_{-3}^1(x^4+9x^2+36+6x^3-12x^2-36x-9-x^2+6x)dx=\\ &\\ &\\ &\\ &\pi \int_{-3}^1(x^4+6x^3-4x^2-30x+27)dx=\\ &\\ &\\ &\\ &\pi \left [ \frac{x^5}{5}+\frac{6x^4}{4}-\frac{4x^3}{3}-15x^2+27x \right ]_{-3}^1=\\ &\\ &\\ &\\ &\pi \left (  \frac{1}{5}+\frac{3}{2} -\frac{4}{3}-15+27+\frac{243}{5}-\frac{486}{4}-36+135+81 \right )=\\ &\\ &\\ &\\ &\pi \left ( 192+\frac{244}{5}+\frac{3}{2}-\frac{4}{3}-\frac{486}{4} \right )=\\ &\\ &\\ &\pi \left ( \frac{11520+2928+90-80-7290}{60} \right )=\\ &\\ &\\ &\frac{7168 \pi}{60} = \frac{1792 \pi}{15}\end{align}$$

Esto es muy pesado, hay que concentrarse mucho y cuesta mucho y el que queda aun es peor.

Para la parte que falta vuelva a mandar la pregunta y la contestaré. Es que hay algunas preguntas que no se pagarían con todo el oro del mundo, no puedo pegarme horas con una sola pregunta.

la parte a) es la que falta? para enviartela