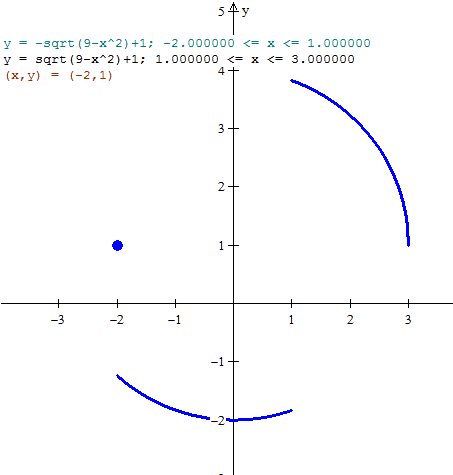Ayuda con la gráfica de esta función
Me podrías explicar el desarrollo de la siguiente función:
Aki esta el link, la función esta donde dice INPUT:
http://www.wolframalpha.com/input/?i=f%28x%29%3D+%5B+%5Bsqrt%289-x%5E2%29%5D*sgn%5B+sqrt%28x%2B2%29+%2F+%28x+-1%29+%5D+%5D%2B+floor+%5B+%282x%2B5%29+%2F+%28x%2B3%29+%5D
EL || (2X+5 )/ (X+3)|| significa máximo entero , o parte entera
Me piden hallar también el rango y el dominio
1 Respuesta
La función sqrt(9-x^2) esa definida en el intervalo [-3,3]
La función sgn es la función signo:
sgn(x) = 1 si x>0
sgn(x) = 0 si x=0
sgn(x) = -1 si x<0
sgn[sqrt(x+2)/(x+1)] El numerador es siempre positivo o cero, la función tiene estos valores
(-infinito, -2) No está definida
en -2 -----> 0
(-2, 1) --> -1
en 1 no está definida
(1, + infinito) ==> 1
Luego el dominio es la intersección de los dominio y queda
Dom f = [-2, 1) U (1,3]
La función floor(x) es la parte entera, máximo entero que no es superior a x. Vamos a examinar lo de dentro de la parte entera. Lo más sencillo es hacer la gráfica para ver que es creciente en [-2, 3], pero si derivamos
[2(x+3)-(2x+5)]/(x+3)^2 = (2x+6-2x-5)/(x+3)^2 = 1/(x+3)^2
es siempre positiva luego la función es siempre creciente
en x-2 vale
||(2x+5)/(x+3)|| = (-4+5)/1= 1
Y el límite en infinito es 2, luego nunca vale 2, asi que valdrá siempre 1 en el dominio
Luego la función total esta definida en [-2, 1) U (1,3] Y su valor es
1 en x=-2
- sqrt(9-x^2) + 1 en (-2,1)
sqrt(9-x^2) + 1 en (1, 3]
Esta gráfica está mejor que la de la página porque salia achatada en ella. Salvo por el punto el resto es parte de una circunferencia de radio 3 y centro (0,1)
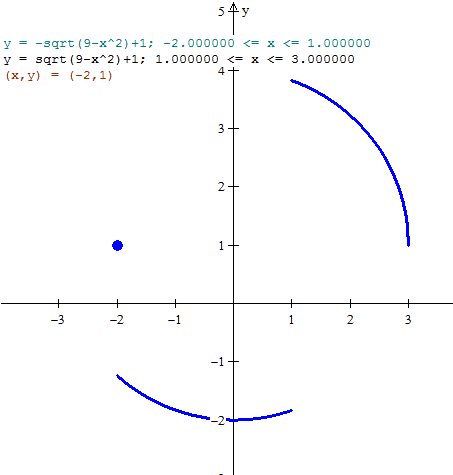
Y esto es todo.
