Graficar la función x/(x^2-1)

Supongo que aparte de la gráfica hecha con algún programa querrás conocer alguno de los datos que se emplean para hacer gráficas.

1) El dominio es todo R salvo los puntos donde el denominador se anula

x^2-1=0

x^2=1

x=+-1

Dom f = R - {-1, 1}

2) Tiene asíntotas verticales en esos puntos donde no está definida, son las rectas x=-1 y x=1

Tiene asíntotas horizontales ya que el límite cuando x tiende a + infinito o - infinito es 0. Luego tiene como asíntota horizontal la recta y=0

3) La derivada es

$$f´(x) = \frac{x^2-1-2x^2}{(x^2-1)^2}=-\frac{x^2+1}{(x^2-1)^2}$$

Es siempre negativa, luego la función es siempre decreciente y no tiene máximos ni mínimos relativos

4) La derivada segunda es

$$\begin{align}&-\frac{x^2+1}{(x^2-1)^2}\\ &\\ &f´´(x)=-\frac{2x(x^2-1)^2-(x^2+1)2(x^2-1)2x}{(x^2-1)^4}=\\ &\\ &-\frac{2x(x^2-1)-4x(x^2+1)}{(x^2-1)^3}=\\ &\\ &-\frac{2x^3-2x-4x^3-4x}{(x^2-1)^3}= \\ &\\ &-\frac{-2x^3-6x}{(x^2-1)^3}= \frac{2x^3+6x}{(x^2-1)^3}\end{align}$$

El signo del numerador es el signo de x. Si x<0 es negativo y si x>0 es positivo

Y el del denominador es el de x^2-1

x^2-1 >= 0

x^2 >= 1

|x| >1

Luego el denominador es negativo en (-1,1) y positivo en el resto

Entonces el signo de la deriva da segunda es

En (-oo, -1) numerador negativo y denominador positivo, resultado negativo

En (-1, 0) numerador negativo y denominador negativo, resultado positivo

En (0, 1) numerador positivo y denominador negativo, resultado negativo

En (1,+oo) numerador positivo y denominador positivo, resultado positivo

Resumiendo, la función es:

Cóncava hacia arriba en (-1,0) U (1, +oo)

Cóncava hacia abajo en (-oo, -1) U (0,1)

5) También sería conveniente conocer los límites laterales de la función en -1 y +1

$$\begin{align}&\lim_{x\to -1_-}\frac{x}{x^2-1}=\frac {signo -}{\gt 0}=-\infty\\ &\\ &\lim_{x\to -1_+}\frac{x}{x^2-1}=\frac {signo -}{\lt 0}=+\infty\\ &\\ &\lim_{x\to 1_-}\frac{x}{x^2-1}=\frac {signo +}{\lt 0}=-\infty\\ &\\ &\lim_{x\to 1_+}\frac{x}{x^2-1}=\frac {signo +}{\gt 0}=+\infty\end{align}$$

Y luego ya tomarías los puntos que necesitaras para dibujarla bien.

(0, 0)

(1/2, -2/3)

(-1/2, 2/3)

(2, 2/3)

(-2, 2/3)

Etc.

La gráfica es esta:

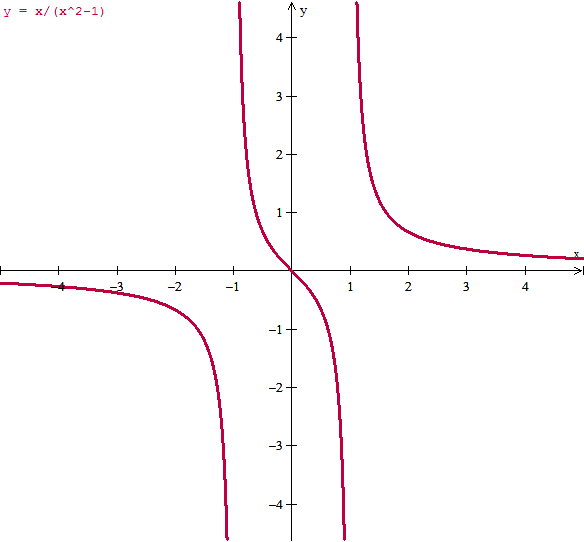
Y eso es todo.

Hola, eso esta excelente, solo que no es lo que yo pedía, no he llegado a TANTO

yo lo que buscaba era algo parecido a esto:

la gráfica, que es una linea recta donde se gráfica el conjunto que satisface la función, pero de todas formas lo que me mandaste esta bien y lo entiendo, gracias.