Círculos en un Rectángulo Parte 2

Lo que haremos será unicamente comprobar si se puede poner una fila o columna más con las condiciones de que las lineas tendrán la misma altura para todos los cilindros. Para ello los cilindros deberán tener una separación igual entre ellos, cosa que puede ser difícil de conseguir en la práctica. Aunque a veces puede haber holgura suficiente y obtenerse el mismo resultado aunque se coloquen juntos todos los cilindros de la fila.

Los cálculos son los que ya hice.

Sea L el largo del rectángulo y H la altura, sea D el diámetro

Sea CF el número entero de cilindros que caben en la fila

CF = parte entera (L / D)

Sea CC el número de cilindros que caben en una columna

CC = parte entera ( H /D)

Llamemos hf el hueco total en la primera fila

hf = L - CF · D

Y sea hc el hueco de la primera columna

hc = H - CC · D

Llamaré

Hfc al hueco en la fila entre cilindros

Hfp al hueco en la fila entre el último cilindro y la pared

Hcc al hueco entre cilindros en la columna

Hcp al hueco en la columna entre el último cilindro y la pared

Para que las filas o columnas estén rectas se debía cumplir

hf = (CF-1)hfc + hfp

hfp = (D+hfc) / 2

luego

hf = (CF-1)·hfc + (D+hfc)/2

2·hf = 2·(CF-1)·hfc + D + hfc

2·hf - D = (2·CF-1)hfc

hfc = (2·hf - D) / (2·CF-1)

Aquí ha surgido un problema imprevisto, para que se pueda poner la segunda fila recta debe ser 2·hf - D > 0, luego el hueco que quede en la fila debe ser mayor qu el radio del cilindro, si no hay que usar otro método. ¡Pues vaya contratiempo más grande!

Sigamos con este método y luego veré qué puede hacerse cuando el hueco sea menor que el radio.

hfp = (D+hfc)/2

Ahora llamare ef a la altura extra por cada fila

ef = sqrt[D^2 - (hfp)^2]

Cálculos análogos nos darían ec, la altura extra para cada columna.

Veamos como es cuando el hueco es inferior al radio

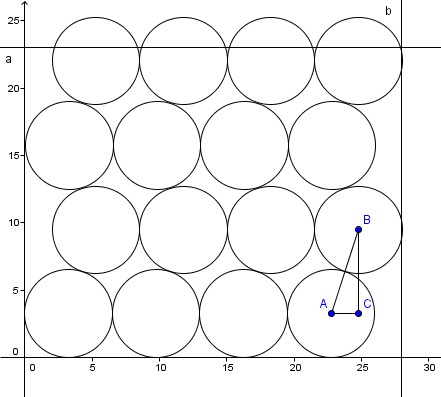
¡Ah, pues quedan rectas! Yo pensaba que no. Lo que pasa es cada cilindro de arriba solo se apoya sobre uno de abajo, mientras que si el hueco era superior al radio se apoyaba sobre 2 y además para optimizar había que hacer huecos entre los cilindros. Y el cálculo de la altura extra por fila es más sencillo incluso.

AC = hc

BC = sqrt(AB^2 - hc^2) = sqrt(D^2 - hf^2)

Vale, pues lo tendremos en cuenta en la fórmula,

si 2hf < D haremos hfc=0 y hfp=hf

Te mando la hoja de cálculo con las celdas de las fórmulas bloqueadas, solo debes introducir datos en las tres primeras columnas. Mejor la miras y si no entiendes algo me lo preguntas.