Como graficar una función inversa

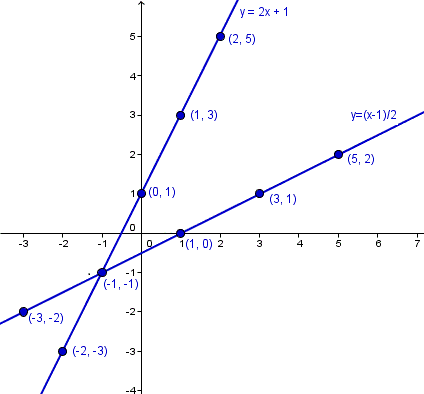
La gráfica de la función

f(x) = 2x+1

Es la de una recta, bastaría conocer dos puntos de la función para hacer la gráfica, pero haremos alguno más.

Damos valores a x y calculamos los valores de f(x) que serán el valor de la coordenada y del punto.

 x |    f(x)    |   (x,y)
--------------------------
-2 | 2(-2)+1=-3 |  (-2,-3)
-1 | 2(-1)+1=-1 |  (-1,-1)
 0 | 2·0+1 = 1  |   (0,1)
 1 | 2·1+1 = 3  |   (1,3)
 2 | 2·2+1 = 5  |   (2,5)

La función inversa es la que a la imagen le hace corresponder el origen. Puedes calcularla despejando la x de esta forma:

y = 2x+1

y-1 = 2x

x = (y-1)/2

Y ahora hay que cambiar los papeles de x por f^-1(x) y de y por x, con lo cual queda

f^(-1)(x) = (x-1)/2

Con ello puedes calcular puntos de la función inversa de igual manera que antes, por ejemplo

f^-1(-2) = (-2-1)/2 = -3/2

Que nos da el punto (-2, -3/2)

Haciendo cálculos en otros puntos nos dará

(-1,-1)

(0,-1/2)

(1,0)

(2,1/2)

Y hay otra forma de tabularla que es intercambiando las coordenadas de los 5 puntos de f(x) que habíamos calculado más arriba:

(-3, -2)

(-1,-1)

(1,0)

(3,1)

(5,2)

Y con estos puntos se hacen las gráficas: