Gráfica de una función calculo
Graficar función que sean derivables a partir de ubicar unos cuantos puntos
significativos. F(x)=x-sen(2x)
1 Respuesta
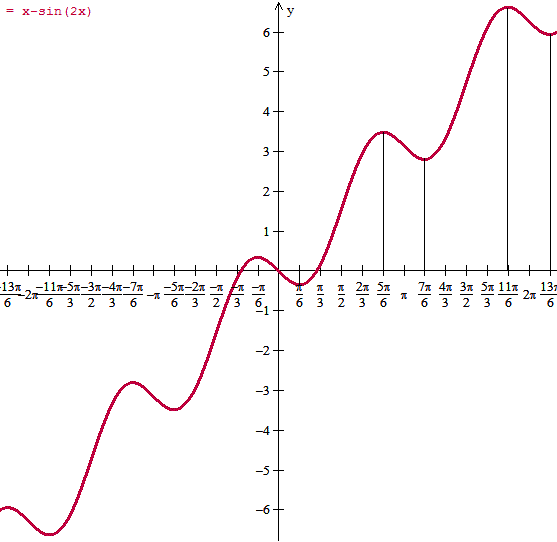
Es una función continua, tiene un corte con los ejes en el punto (0, 0) y los otros son difíciles de calcular. No tiene asíntotas de ningún tipo.
Veamos los máximos, mínimos, zonas de crecimiento y decrecimiento, para ello la derivamos e igualamos a cero
f '(x) = 1 - 2 cos(2x) = 0
2cos(2x) = 1
cos(2x) = 1/2
2x = pi/3 , 5pi/3, 7pi/3 , 11pi/3
x = pi/6 , 5pi/6, 7pi/6 , 11pi/6
En [0, pi/6) tomamos x=0 entonces f '(x)=1-2 = -1 luego f es decreciente
en (pi/6, 5pì/6) tomamos x=pi/2 entonces f '(x) = 1+2=3 luego f creciente
en (5pi/6, 7pi/6) tomamos x=pi entonces f '(x) = 1-2 =-1 luego f decreciente
en (7pi/6, 11pi/6) tomamos x=3pi/2 entonces f '(x) = 1+2 luego f creciente
en (11pi/6, 2pi] tomamos x=2pi entonces f '(x) = 1-2=-1 luego f es decreciente
f ''(x) = 4 sen(2x)
4sen(2x)=0
sen(2x) = 0
2x = 0, pi, 2pi, 3pi
x = 0, pi/2, pi, 3pi/2
en [0, pi/2) tenemos f ''(x) = 4sen(2x) > 0 luego f cóncava hacia arriba
en (pi/2, pi) tenemos f ''(x) =4sen(2x) < 0 luego f cóncava hacia abajo
en (pi, 3pi/2) es cóncava hacia arriba
en (3pi/2, pi) es cóncava hacia abajo
F ''(pi/6) = 4sen(pi/3) >0 luego pi/6 es mínimo
f ''(5pi/6) = 4sen(5pi/3) < 0 luego 5pi/6 es máximo
f ''(7pi/6) = 4sen(7pi/3) >0 luego 7pi/8 es mínimo
f ''(11pi/6) =4sen(11pi/3) < 0 luego 11pi/6 es máximo
Y todos estos máximos, mínimos, crecimientos, decrecimientos y concavidades se repiten cada 2pi a diferente altura
Y eso es todo.
Gracias muy claro!
No sé si será fallo de la página o que va con retraso. Pero si has puntuado no han llegado los puntos.
