Figura geométrica con triángulos semejantes
Hola valeroasm, un gusto saludarlo. Me podría decir los métodos que puedo utilizar para averiguar el segmento EF de la siguiente figura. Y como usted lo resolvería. Gracias de antemano. 
1 Respuesta
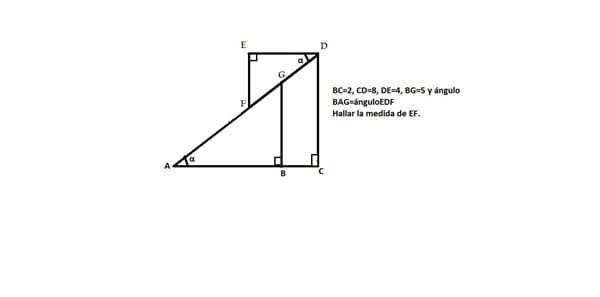
Los triángulos ACD y DEF son semejantes por ser rectángulos y tener un ángulo igual. Además fíjate que el orden en que he puesto las letras se corresponde con los ángulos iguales.
Por el teorema de Thales
AC/DE = CD/EF
Veamos cuáles son los datos conocidos
AC/4 = 8/EF
EF = 8·4/AC = 32/AC
Luego para conocer EF necesitamos conocer AC
Por otro lado ACD también es semejante a ABG por tener un ángulo común y los lados opuestos paralelos. Aplicando de nuevo el teorema de Thales
AC/AB = CD/BG
también tenemos
AC = AB + BC = AB + 2
con lo que la igualdad anterior es
(AB+2)/AB = 8/5
llamemos x=AB para resolver más cómodamente la ecuación
(x+2)/x = 8/5
5(x+2)=8x
5x + 10 = 8x
3x = 10
x = 10/3
AB=10/3
luego
AC = AB + 2 = 10/3 + 2 = 16/3
AC = 16/3
y ahora vamos a la igualdad de más arriba
EF = 32/AC = 32 / (16/3) = (32·3) / 16 = 3
Luego EF = 3
No te fíes del dibujo, no se corresponde con la realidad, el angulo alfa es bastante más grande.
Y eso es todo.
