Explicar las funciones es un tema muy extenso, además tampoco sé hasta que nivel tendría que explicarte. Eso es mejor que lo estudies en los libros de texto adecuados al nivel que te piden. Contestar preguntas concretas o solucionar ejercicios sí puedo hacerte cuantos quieras.
Vamos con este:
a)
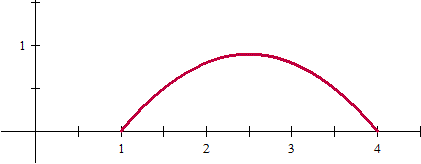
En el eje Y los tantos por ciento están expresados como número, es decir, ya divididos por 100. Eso es lo que significa un % al fin y al cabo, un número dividido por 100.
Y lo he hecho así porque si lo poníamos de la otra forma, con números entre 0 y 100 la curva salía tan alta que no cabía, o si cabía de altura era tan estrecha que no se veía.
b) El rendimiento máximo parece darse en el punto medio, podría verificarse que es simétrica respecto de el, pero el problema está enfocado a que resuelvas el problema con la teoría de máximos y mínimos.
Hay que hallar los puntos donde la derivada primera se anula
f(t) = 40(1-t)(t-4)
f '(t) = 40[(-1)(t-4) +1(1-t)] = 4(-t+4+1-t) = 4(5-2t)
Y la derivada es cero cuando
4(5-2t) = 0
5-2t=0
5 = 2t
t = 5/2
Efectivamente es 2.5 el punto intermedio.
Y el máximo es
f(2.5) = 40(1-2.5)(2,5-4) = 40(-1.5)(-1.5) = 90%
c) Estará dos veces por lo qu vemos en la gráfica. vemos a calcularlo
80 = 40(1-t)(t-4)
Dividimos por 40 antes de nada
2 = (1-t)(t-4)
2 = t - 4 -t^2 + 4t
Operamos y ordenamos
2 = -t^2 + 5t - 4
Todo a la izquierda
t^2 -5t + 6 = 0
Resolvemos la ecuación de segundo grado, no te asustes por el sqrt, significa raíz cuadrada en las normas estándar internacionales.
t = [5 +- sqrt(25 - 24)]/ 2 = [5 +- sqrt(1)]/2 = (5 +- 1)/2
t1 = 3
t2 = 2
Luego en t= 2 y t=3 se está al 805 de rendimiento
d) Hay aumento de rendimiento en la primera mitad, hasta que se llega al máximo, luego en el intervalo
1 < t < 2,5
El 2,5 evidentemente no entra porque el aumento de rendimiento es cero
El 1 tampoco entrá porque no está definida la función antes, pero si se supone que era la función cero entonces no hay aumento.


