Resuelve el siguiente problema de conexidad 1
Considera:
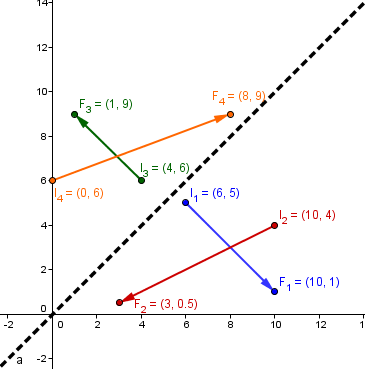
$$\begin{align}&CS^2 (R)=R^2∖Δ\end{align}$$el espacio de configuraciones seguras de dos robots A y B moviéndose en una línea. Observa la ilustración:
para que recuerdes cuál es este espacio.
Para cada uno de los siguientes casos dibuja un segmento de línea en :
$$\begin{align}&CS^2 (R)\end{align}$$que represente la situación y el traslado descrito. Utiliza la notación:
$$\begin{align}&(I_A,I_B) \end{align}$$para la posición inicial de los robots y:
$$\begin{align}&(F_A,F_B) \end{align}$$para la posición final.
1.- El robot B está a la izquierda del robot A y se mueven en direcciones opuestas, alejándose uno del otro.
2.- El robot B está a la izquierda del robot A y ambos se mueven a la izquierda. El robot B avanza más que el robot A.
3.- El robot A está a la izquierda del robot B y se mueven en direcciones opuestas, alejándose entre ellos.
4.- El robot A está a la izquierda del robot B y ambos se mueven hacia la derecha. El robot A se desplaza más que el robot B.
1 Respuesta
Hola buenas tardes, le acabo de enviar a su correo, algo de teoría respecto al problema, espero me pueda ayudar si no de todas maneras se lo agradezco mucho ya que me ha apoyado bastante.
saludos.
Es que esto de los robots sin el documento que me has dado no había quien supiera que era.
1) El robot B a la izquierda luego la segunda componente tiene un número menos que la primera, por ejemplo una posición inicial (6,5) y como se mueven en direcciones opuestas llegan a (10,1)
2) Al igual que antes la segunda componente es menor que la primera
Por ejemplo (10,4) Y se mueven a laizquierda luego restana cada paso, pongamos que el robot B va al doble de velocidad, el punto de llegada puede ser (2,0)
3) Este es como el caso 1 pero ahora la componente primera es menor. Punto de inicio (4,6) punto de llegada (1,9)
4) La componente primera es menor, el desplazamiento hace aumentar las dos pero más la primera. Por ejempo (0,6) a (8,9) Aquí la realción de velocidad me ha salido 8/3, me equivoqué porque queríoa poner 2 pero sirve igual, es que ya tengo hecho el gráfico.
Y eos es todo.
Amo Mo!
Debes puntuar la pregunta.
