Son todo cosas teóricas que pensaba que a lo mejor las sabías y por eso no lo explicaba y me limitaba a hacer los cálculos.
La varianza de X (que se simboliza por sigma cuadrado) se calcula así:
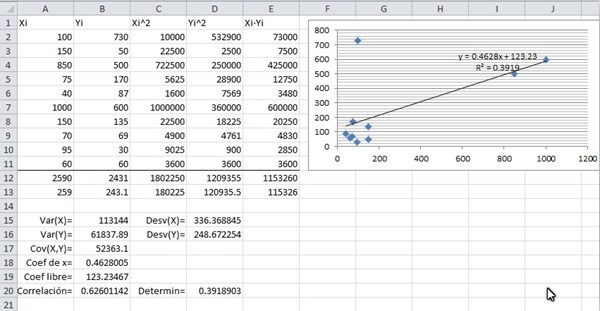
$$\begin{align}&\sigma_X^2=\frac{\sum_{i=1}^n X_i^2}{n}-\mu_X^2\end{align}$$Entonces tienes la columna C donde están los cuadrados de las Xi desde C2 a C11, en C12 está la suma y en C13 la división entre 10. Eso te da el primer término y luego le restas el cuadrado de la media de los Xi que está en A13.
La varianza de Y es lo mismo pero referido a la columna D y con la media de B13
La Covarianza de X y Y se calcula así.
$$\begin{align}&Cov(X,Y)=\frac{\sum_{i=1}^n X_iY_i}{n}-\mu_X·\mu_Y\end{align}$$Entonces en la columna E están los productos Xi·Yi, en E12 la suma y en E13 el promedio. A ese E13 hay que restarle el producto de las medias que están en A13 y B13
El coeficiente de X y el coeficiente libre son números que se calculan a partir de esta fórmula una vez que haces las operaciones, arriba te lo explicaba, vuelvo a poner las cuentas.
$$\begin{align}&y=\overline y+\frac{Cov(X,Y)}{\sigma_X^2}(x-\overline x)\\ &\\ &y = 243.1+\frac{52363.1}{113144}(x-259)\\ &\\ &y = 243.1+0.4628(x-259)\\ &\\ &y =243.1 + 0.4628x - 119.8652\\ &\\ &y = 0.4628x + 123.2348\end{align}$$Cuando te pase la hoja te fijas cual es la expresión exacta ya calculada para los coeficientes.
Las desviaciones no son otra cosa que la raíz cuadrada de la varianza correspondiente, es por eso que se escriben con el símbolo sigma ya que la varianza tiene el símbolo sigma cuadrado.
Y el coeficiente de correlacióny determinación te explicaba como se calculaban en el otro ejercicio.
Cuando te mande la hoja puedes usarla par hacer otras correlaciones si añades o quitas filas con cuidado. Siempre deben empezar los datos en la fila 2, tú tienes que escribir los datos en las columnas A y B hasta la línea de separación.
Si quieres añadir filas tienes que usar Añadir Filas para que así las nuevas hereden las fórmulas.
Y no escribas sobre ninguna celda de las que tienen fórmulas.
T debe haber siempre una línea de separación entre los promedios y las celdas de abajo.
Haz una copia y no trabajes nunca sobre el original por si machacas alguna fórmula.
Espera un poco que tardaré en mandártela porque estoy haciendo que pueda calcular también las previsiones de Y para un valor de X y viceversa.