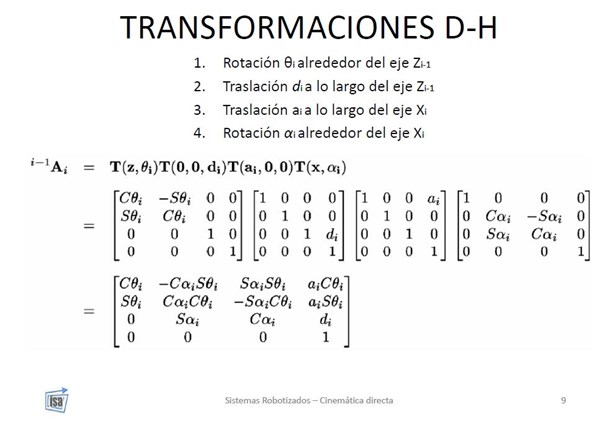
Matrices y geometría (transformación)
Quería pedirte ayuda para que me indicaras como sería la resolución de este ejercicio, ya que tengo un poco planteado el inicio de la resolución que hizo el profesor en clase, pero no se como continuar a partir de ese punto.
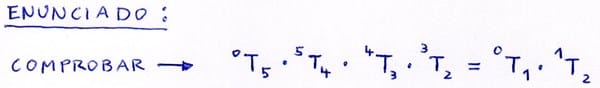
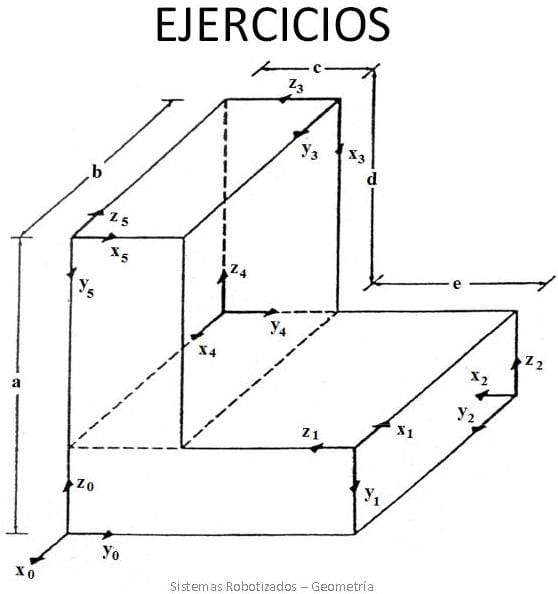
El profesor dijo que se podía resolver de dos formas diferentes, una desde el punto de vista del eje fijo y otra desde el punto de vista del eje móvil. Y que depende de la que elijamos tendremos que pre-multiplicar o pos-multiplicar.
Llegados a este punto se que las dos 0T5 que he obtenido son validas para continuar, y debo elegir una para a partir de la función que tengo generar tres matrices que se multiplicaran, pero no se como generarlas con los datos que tengo.
Aunque si se que para ello debo de utilizar lo siguiente:
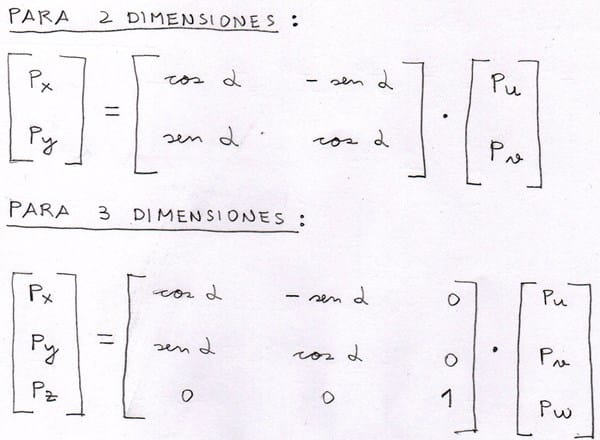
Se que el ejercicio es bastante largo, pero me podrías indicar como se continuaría a partir de este punto??
1 Respuesta
Tengo las teoría del tema respecto a esto. Me igagino que para alguien que sepa trabajar con vectores y matrices no debe ser nada complicado matemaricamente.
¿Exiete forma de poder enviártelo a algún correo o lectronico o algo así?
Gracias por anticipado.
Si puedes prefiero que cuelgues la teoría en un lugar de intercambio como Dropbox, Google Drive u otro y escribas el enlace.
Te pongo aquí un enlace (acceso libre) al archivo de mi dropbox. Es un archivo pdf.
https://www.dropbox.com/s/9srp80oterq6wp7/GEOMETRIA%20_Modo%20de%20compatibilidad_.pdf?dl=0
No creo que haya problema, pero por si acaso no pudieras abrirlo, no dudes en avisarme.
Gracias de nuevo.
Si, he podido descargarlo, pero no sé si con eso será suficiente sin saber nada de robótica. Sigo sin entender la notación T(0,0, a), ¿significa traslación de vector (0,0, a)?
Y los 0T5 y de ese tipo me parece que tampoco explica lo que son.
Es un poco complicado, ahora no puedo verlo.
si, es una translacion de la distancia que llama (a)
Respecto a lo que me comentaste que no tenias muy claro, he encontrado esta teoría, que a lo mejor te es de más ayuda para intentar ayudarme a resolver el problema.
En algún sítio te pondrá que una rotación y una traslación conmutan, luego podemos poner todas las traslaciones al principio o al final.
Se comprueba fácilmente que el resultado de las traslaciones es el mismo
La traslación para
0T5 es (0, 0, a)
5T4 es (-b, 0, -d)
4T3 es (0, c, d)
3T2 es (0, e, -a)
la composición de las cuatro es su suma
(-b, c+e, 0)
Y por el otro camino las tralaciones son
0T1 es (0, c+e,a-d)
1T2 es (-b, 0,d-a)
cuya suma es
(-b, c+e, 0)
Luego la traslación es la misma, esta era la parte fácil.
Y quedaría ver que el resultado de los giros es el mismo de las dos formas. Pero yo no sé si hay teoría al respecto o tienes que multiplicar las matrices, se puede hacer eterno.
