Calcular el volumen de un sólido mediante la doble integración
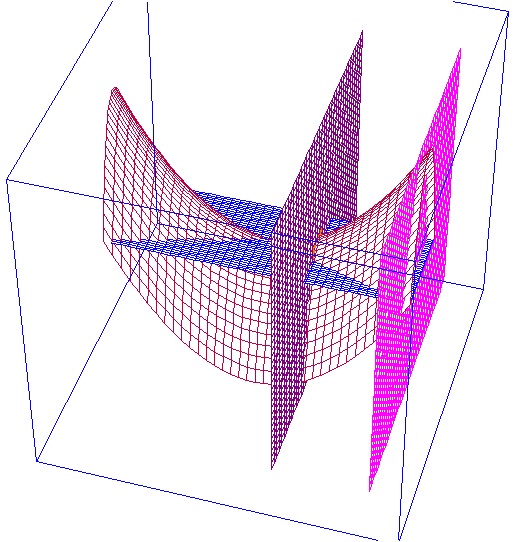
Sólido que está limitado por la superficie z=x^2-y^2, el plano xy, y los planos x=1 y x=3. Calcular entonces el volumen mediante doble integración
1 respuesta
Laura Aleenah!
·
La gráfica no es muy buena, hace años que ando buscando un programa sencillo que haga gráficas 3D buenas pero no lo encuentro, no obstante ayuda bastante a entender el problema.
El plano xy es el plano z=0, veamos la intersección que tiene con la superficie
0 = x^2 - y^2
y^2 = x^2
Esto son dos rectas
y=x
y = -x
Con todo esto el volumen es:
$$\begin{align}&V=\int_1^3\int_{-x}^x(x^2-y^2)dy dx =\\ &\\ &\int_1^3\left[x^2y-\frac{y^3}{3} \right]_{-x}^x dx=\\ &\\ &\int_1^3\left(x^3-\frac {x^3}{3} +x^3-\frac{x^3}{3} \right)dx=\\ &\\ &\int_1^3 \frac 43x^3dx=\\ &\\ &\frac 43·\frac{x^4}{4}\left. \right|_1^3=\frac 43\left(\frac{81}{4}-\frac 14 \right)=\frac {80}{3}\end{align}$$Y eso es todo.
¡Gracias! Maestro Valero, no sé porqué ya no me dejan preguntarle directo sobre su perfil, ahora asignan expertos y a la siguiente pregunta que hice no me han dejado agregarle a Usted.
Hay algo de oscurantismo en esta página, como normas que no conocemos y solo nos damos cuenta cuando descubrimos que nos han sancionado sin avisarnos. Otras veces son fallos puntuales. No conozco yo la norma que impida que preguntes a un experto concreto.
